En la geometría de triángulos, los puntos notables juegan un papel fundamental al revelar propiedades y características únicas de estas figuras. Son puntos especiales que se derivan de las líneas notables del triángulo, como las medianas, alturas, bisectrices y mediatrices. Los puntos notables más comunes y destacados son el baricentro, ortocentro, incentro y circuncentro.

Estos puntos notables proporcionan información valiosa sobre la forma, simetría y propiedades del triángulo. Además, se utilizan en diversos campos, como la resolución de problemas geométricos, la construcción de figuras y en aplicaciones prácticas en arquitectura, ingeniería y diseño. Al comprender la importancia de los puntos notables en la geometría de triángulos, se abre la puerta a un mayor conocimiento y apreciación de esta rama de las matemáticas.

Triángulos y sus puntos notables: Un viaje por la belleza de la geometría

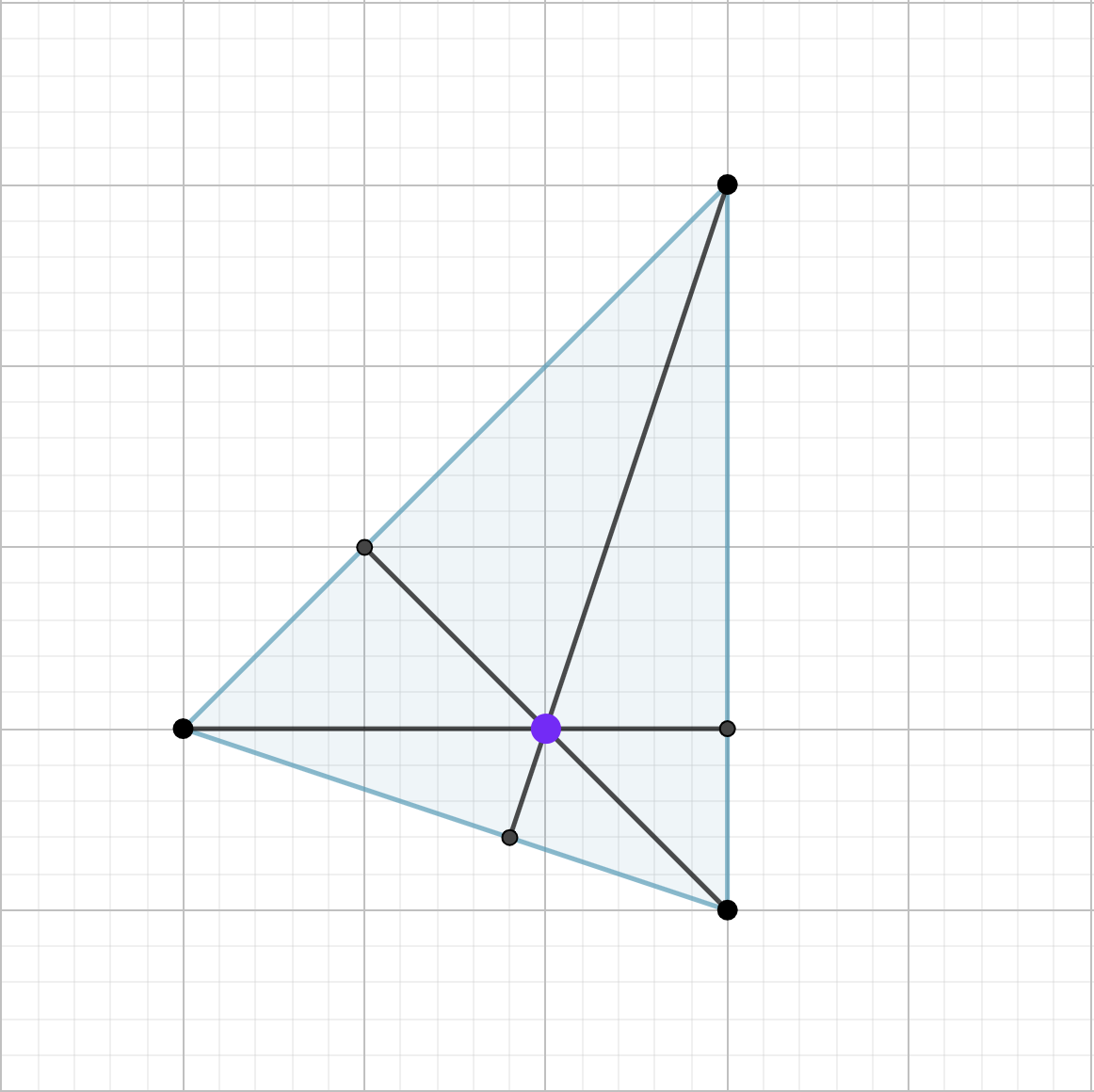
Baricentro

El baricentro, también conocido como centroide, es el punto de intersección de las tres medianas de un triángulo. 

Una mediana es un segmento de recta que une un vértice con el punto medio del lado opuesto. Las medianas dividen al triángulo en seis triángulos de igual área.

El baricentro tiene propiedades interesantes:

• El baricentro divide cada mediana en dos segmentos en la relación 2:1. Es decir, la distancia desde un vértice al baricentro es el doble que la distancia desde el baricentro al punto medio del lado opuesto.
• El baricentro es el centro de gravedad del triángulo. Si consideramos que los vértices tienen masas iguales, el baricentro es el punto donde el triángulo se equilibra.
• El baricentro es siempre el punto interior del triángulo.

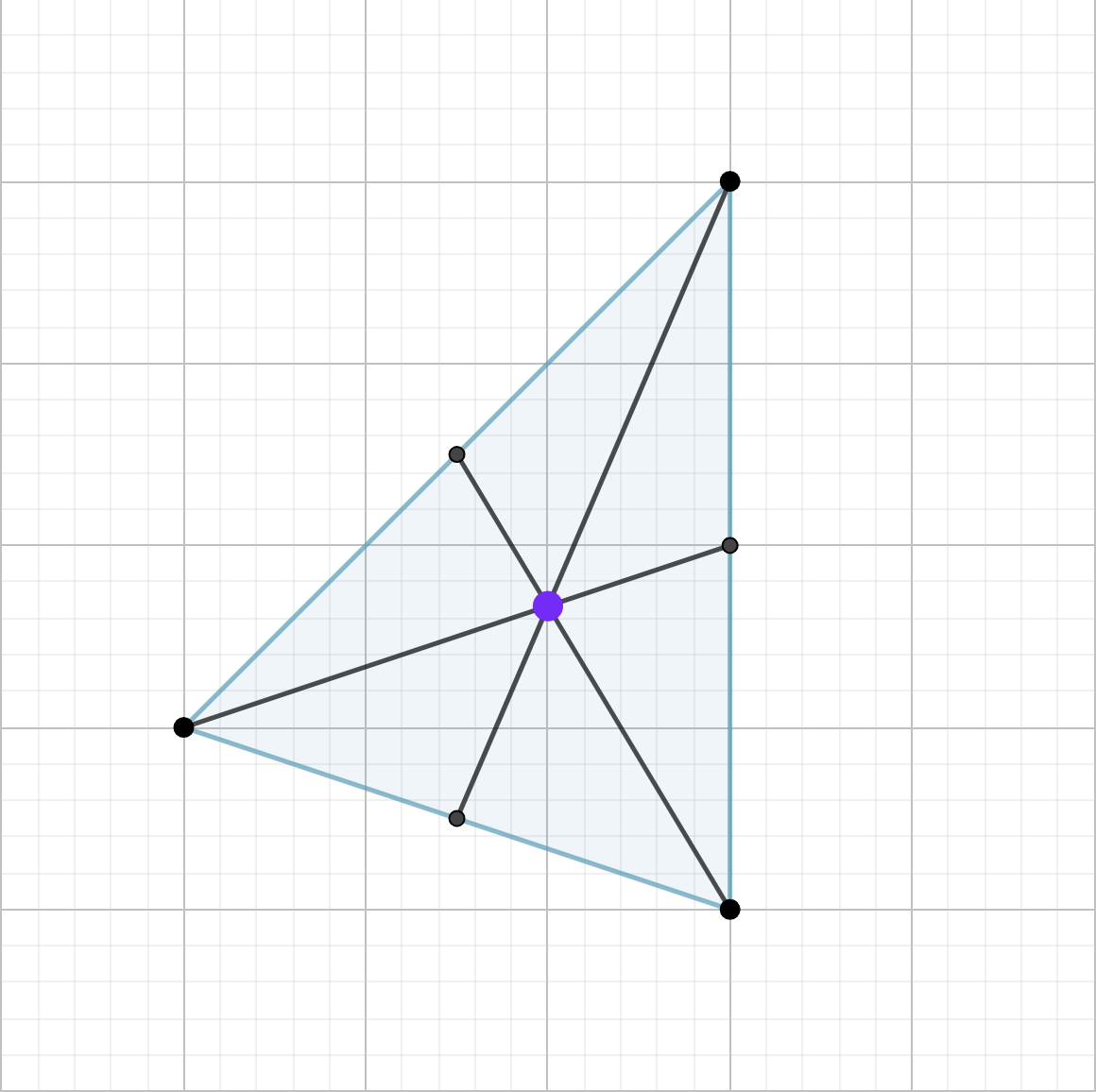
Ejemplos y aplicaciones prácticas

• En arquitectura y construcción, el baricentro se utiliza para determinar la posición óptima del centro de gravedad de una estructura y distribuir adecuadamente el peso
• En diseño de objetos y elementos visuales, el baricentro se utiliza para lograr equilibrio visual y simetría en composiciones gráficas o artísticas
• En ciencia de materiales y mecánica, el baricentro es fundamental para analizar y comprender el comportamiento de objetos tridimensionales sometidos a fuerzas y momentos
• En problemas geométricos, el baricentro es un punto clave para determinar propiedades como la concurrencia de rectas o el cálculo de áreas en triángulos

Ortocentro

El ortocentro es el punto de intersección de las tres alturas de un triángulo. Una altura es un segmento de recta perpendicular a un lado del triángulo que pasa por el vértice opuesto. 

Las propiedades del ortocentro son:

• El ortocentro puede estar ubicado dentro del triángulo, en uno de sus vértices o incluso fuera del triángulo, dependiendo de la forma del triángulo
  • Si el triángulo es acutángulo (todos sus ángulos internos son agudos), el ortocentro estará dentro del triángulo
  • Si el triángulo es obtusángulo (uno de sus ángulos internos es obtuso), el ortocentro estará fuera del triángulo
  • Si el triángulo es equilátero, el ortocentro coincidirá con los tres vértices del triángulo
  • Si el triángulo es isósceles, el ortocentro estará en la altura que es también la bisectriz del ángulo opuesto al lado desigual.

Ejemplos y aplicaciones prácticas

• En arquitectura y construcción, el ortocentro es crucial para determinar la estabilidad y resistencia de una estructura
• En navegación marítima o aérea, la determinación precisa de la posición es esencial. El concepto del ortocentro se aplica en la triangulación, que utiliza ángulos y distancias para determinar la ubicación de un barco, avión u otro objeto en movimiento
• En diseño de objetos y estructuras, el ortocentro se utiliza para lograr un equilibrio visual y simétrico
• En el campo de la mecánica y la ciencia de materiales, el ortocentro es relevante para analizar el comportamiento de objetos tridimensionales bajo cargas y fuerzas
• En fotogrametría, el ortocentro es utilizado para corregir las distorsiones que surgen al mapear imágenes aéreas o fotografías.
• En cartografía, el ortocentro se utiliza para definir proyecciones y sistemas de coordenadas en mapas, lo que permite una representación más precisa de la superficie terrestre

Incentro

El incentro es el punto de intersección de las tres bisectrices internas de un triángulo. Una bisectriz interna es una recta que divide un ángulo en dos ángulos congruentes.

El incentro tiene propiedades interesantes:

• El incentro es equidistante de los tres lados del triángulo. Esto significa que la distancia desde el incentro hasta cada uno de los lados es igual
• El incentro es el centro de la circunferencia inscrita en el triángulo. La circunferencia inscrita es la única circunferencia que pasa por los tres vértices del triángulo y que se encuentra en el interior del triángulo
• Las bisectrices internas dividen al triángulo en tres triángulos más pequeños, cada uno de los cuales tiene al incentro como su centro de incírculo
• El incentro es el punto de simetría de las tangentes trazadas desde los vértices del triángulo a la circunferencia inscrita

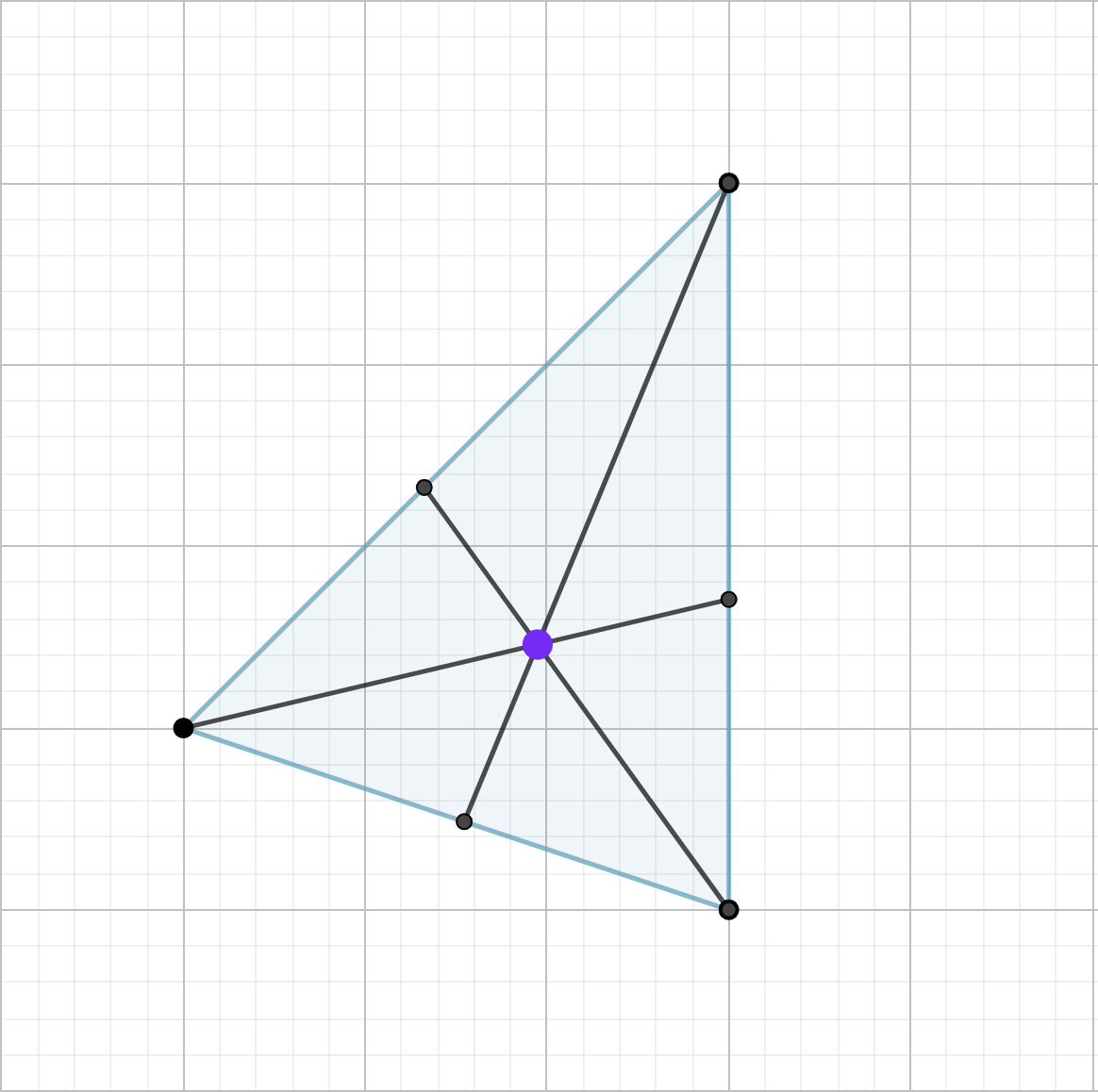
Ejemplos y aplicaciones prácticas

• El incentro es fundamental para el cálculo del área de un triángulo mediante la fórmula de Herón
• Al trazar las bisectrices de los ángulos de un triángulo, se puede utilizar el incentro para construir ángulos trisectores, dividiendo un ángulo en tres partes iguales
• El incentro proporciona información valiosa sobre las propiedades geométricas del triángulo, como la congruencia y semejanza con otros triángulos. 
• En la industria de la moda, el incentro se utiliza en el diseño de patrones y cortes
• La circunferencia inscrita en el triángulo, centrada en el incentro, se utiliza en el diseño de joyas y ornamentos

Circuncentro

El circuncentro es el punto de intersección de las tres mediatrices de un triángulo. Una mediatriz es una recta perpendicular a un lado del triángulo que pasa por el punto medio de dicho lado. El circuncentro también está relacionado con la circunferencia circunscrita, que es la circunferencia que pasa por los tres vértices del triángulo.

Las propiedades y particularidades del circuncentro son:

• El circuncentro está equidistante de los tres vértices del triángulo. Esto significa que la distancia desde el circuncentro hasta cada vértice es la misma
• El circuncentro es el centro de la circunferencia circunscrita al triángulo. La circunferencia circunscrita es única y pasa por los tres vértices del triángulo
• Si el triángulo es equilátero, el circuncentro coincide con el baricentro y el ortocentro del triángulo.

Ejemplos y aplicaciones prácticas

• Conociendo el circuncentro, se puede construir fácilmente la circunferencia circunscrita al triángulo
• El circuncentro es útil para demostrar propiedades de congruencia entre triángulos
• El circuncentro se utiliza en la resolución de problemas geométricos, como el cálculo de áreas y perímetros de triángulos
• En diseño y arquitectura, el circuncentro se utiliza para lograr simetría y equilibrio visual en estructuras y elementos decorativos

La recta de Euler

La recta de Euler es una línea que pasa por tres puntos notables de un triángulo: el baricentro, el ortocentro y el circuncentro. Esta recta recibe su nombre en honor al matemático suizo Leonhard Euler, quien descubrió esta importante relación geométrica.

La recta de Euler tiene varias propiedades notables:

• El ortocentro, el circuncentro y el baricentro siempre están alineados en la recta de Euler. Esto significa que la recta pasa a través de los tres puntos mencionados
• La recta de Euler puede estar tanto dentro del triángulo como fuera de él, dependiendo de la forma del triángulo.
  • En un triángulo equilátero, la recta de Euler pasa por el centro del triángulo

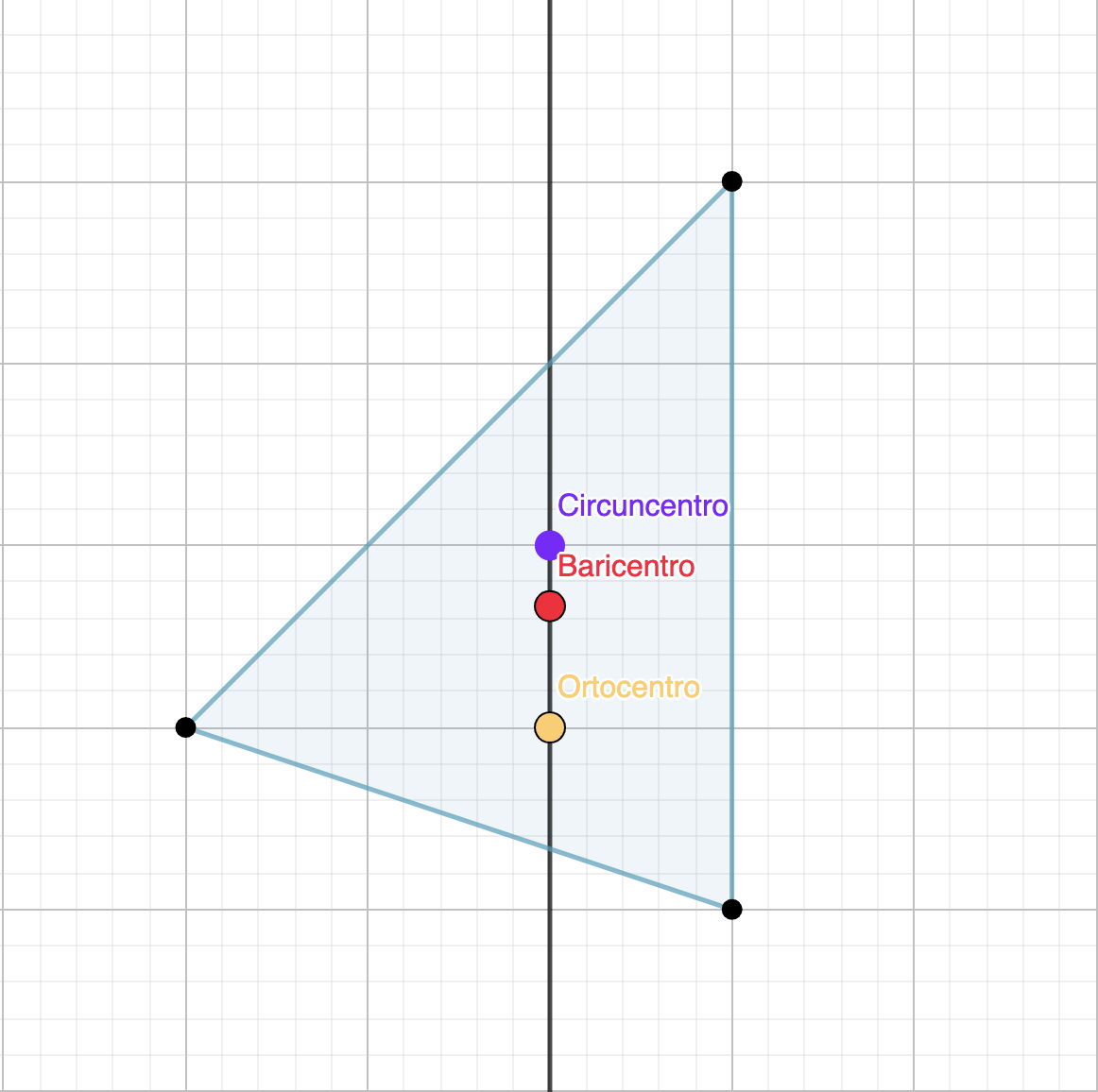
La recta de Euler es una característica interesante de los triángulos y muestra una conexión profunda entre los puntos notables. Su estudio permite comprender mejor las propiedades geométricas del triángulo y su relación con otros elementos, y se utiliza en diversos contextos, como la resolución de problemas geométricos y el diseño arquitectónico.

Conclusiones

El conocimiento de los puntos notables del triángulo es fundamental en geometría, ya que proporciona una comprensión profunda de las propiedades y relaciones geométricas de esta figura. Estos puntos clave permiten realizar cálculos precisos, resolver problemas geométricos y establecer conexiones entre diferentes elementos del triángulo. Además, el estudio de los puntos notables ayuda a desarrollar habilidades de razonamiento espacial, visualización y abstracción, que son valiosas en matemáticas y otras disciplinas científicas.

Matemáticas en Frogames

Descubre un mundo de posibilidades matemáticas con la ruta de cursos "Aprende Matemáticas desde Cero" de Frogames. Desde los conceptos básicos hasta niveles avanzados, nuestra ruta te llevará de la mano a través de un fascinante viaje de descubrimiento matemático.