RMSProp, que significa Root Mean Square Propagation, es un algoritmo de optimización ampliamente utilizado en aprendizaje profundo. Es una mejora sobre AdaGrad (Algoritmo de Gradiente Adaptativo) y soluciona algunas de las limitaciones clave de AdaGrad, especialmente para modelos que trabajan con datos dispersos. En este artículo, exploraremos Root Mean Square Propagation, veremos sus beneficios y cómo funciona con ejemplos prácticos.

¿Qué es Root Mean Square Propagation?

RMSProp fue introducido para resolver un problema inherente a AdaGrad: la disminución de la tasa de aprendizaje. Mientras que AdaGrad adapta la tasa de aprendizaje en función de la acumulación del gradiente para cada parámetro, tiende a reducir la tasa de aprendizaje de manera demasiado drástica con el tiempo, lo que hace que el modelo deje de aprender de manera efectiva.

¿Por qué lo necesitamos?

Primero discutamos brevemente el desafío de AdaGrad. AdaGrad funciona bien con datos dispersos, es decir, datos donde muchos valores son cero. Sin embargo, a medida que avanza el aprendizaje, la tasa de aprendizaje se vuelve tan pequeña que prácticamente deja de hacer actualizaciones, especialmente en modelos con sesiones de entrenamiento largas o funciones de pérdida no convexas (como en redes neuronales). RMSProp ayuda a superar esto ajustando la tasa de aprendizaje de una manera diferente.

¿Cómo funciona este algoritmo?

Root Mean Square Propagation realiza un seguimiento de un promedio exponencialmente decreciente de los gradientes al cuadrado. En lugar de acumular todos los gradientes cuadrados pasados como lo hace AdaGrad, RMSProp utiliza un promedio móvil. Esto significa que RMSProp da más peso a los gradientes recientes, permitiéndole adaptarse de manera más efectiva sin reducir la tasa de aprendizaje demasiado rápido.

La fórmula de Root Mean Square Propagation puede escribirse como:

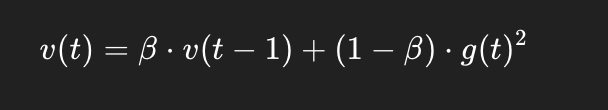
Donde:

• $v(t)$ es el promedio acumulado móvil de los gradientes al cuadrado en el tiempo $t$.

• $\beta$ es una tasa de decaimiento, típicamente alrededor de 0.9 o 0.95.

• $g(t)$ representa el gradiente en el tiempo $t$.

Usando esto, la regla de actualización para cada parámetro $\theta$ se convierte en:

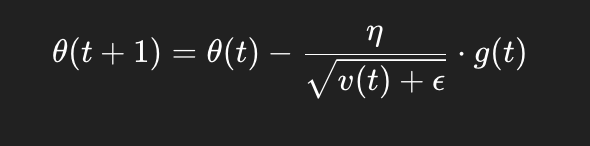
Donde:

• $\eta$ es la tasa de aprendizaje,

• $ϵ$ es una constante pequeña añadida para evitar la división por cero.

Ejemplo de Root Mean Square Propagation en acción

Imagina que estamos entrenando una red neuronal para reconocer dígitos escritos a mano. Cada vez que actualizamos la red, los gradientes apuntan en la dirección que minimiza la pérdida. Con AdaGrad, a medida que avanzan las actualizaciones, la tasa de aprendizaje puede disminuir demasiado, deteniendo el entrenamiento.

Usando RMSProp, el promedio móvil de los gradientes al cuadrado permite que la tasa de aprendizaje se mantenga estable a través de las iteraciones. La red aprende de manera constante sin una desaceleración drástica, logrando finalmente un mejor rendimiento.

Comparación visual: AdaGrad vs. RMSProp

En la práctica, al optimizar un modelo en un gráfico de contorno (un mapa de valores de pérdida), la trayectoria de AdaGrad puede mostrar un movimiento lento o "atascarse" a medida que la tasa de aprendizaje disminuye. En contraste, el promedio decreciente de Root Mean Square Propagation mantiene la tasa de aprendizaje más estable, permitiendo una convergencia más suave y rápida hacia el mínimo de la función de pérdida.

Imagina que AdaGrad toma caminos más largos hacia el mínimo debido a su reducción de paso. Root Mean Square Propagation, por otro lado, da pasos más dirigidos, navegando por el paisaje de manera más efectiva, incluso en modelos complejos como las redes neuronales.

Ventajas

• Eficiente con problemas no convexos: Funciona bien con problemas de optimización complejos y no convexos, comunes en el aprendizaje profundo, a diferencia de AdaGrad, que funciona mejor en entornos convexos.

• Tasa de aprendizaje estable: Previene que la tasa de aprendizaje disminuya demasiado rápido, permitiendo que el optimizador se mueva de manera constante hacia el mínimo.

• Rendimiento comprobado empíricamente: Es ampliamente utilizado en la práctica debido a su robustez y estabilidad en una variedad de arquitecturas de redes neuronales.

Desventajas

Aunque Root Mean Square Propagation es un optimizador muy efectivo, ha sido en gran medida superado por Adam (Estimación de Momento Adaptativo), que combina los beneficios de RMSProp y Momentum (otra técnica de optimización). Adam generalmente supera a Root Mean Square Propagation, pero viene con una sobrecarga computacional adicional.

¿Cuándo usar Root Mean Square Propagation?

• Redes Neuronales Recurrentes (RNNs): RMSProp es especialmente útil en RNNs y otros modelos propensos a gradientes que desaparecen o explotan.

• Datos dispersos: RMSProp maneja datos dispersos de manera efectiva, ajustando las tasas de aprendizaje dinámicamente según los valores recientes de los gradientes.

Reflexiones finales

Root Mean Square Propagation es una herramienta poderosa y ampliamente utilizada para entrenar redes neuronales, ya que proporciona un equilibrio eficaz entre la velocidad de convergencia y la estabilidad durante el proceso de optimización. Este algoritmo ajusta dinámicamente la tasa de aprendizaje para cada parámetro, lo que ayuda a mitigar problemas comunes como los gradientes explosivos o desvanecientes. 

Aunque en la actualidad optimizadores más avanzados como Adam han ganado mayor popularidad por su rendimiento generalizado y facilidad de uso, comprender a fondo el funcionamiento y las ventajas de RMSProp sigue siendo fundamental. Su eficacia es particularmente notable cuando se trabaja con modelos de aprendizaje profundo aplicados a datos dispersos, funciones altamente no convexas o en escenarios donde otros métodos pueden fallar en mantener una actualización estable y eficiente de los pesos.

Resumen

Root Mean Square Propagation adapta las tasas de aprendizaje basándose en un promedio móvil de los gradientes al cuadrado, permitiendo que los modelos aprendan de manera constante sin la drástica reducción de la tasa de aprendizaje de AdaGrad. Sigue siendo una opción popular en la comunidad de aprendizaje profundo, especialmente para redes neuronales recurrentes y conjuntos de datos dispersos.

¡Eso es todo para nuestra exploración profunda de Root Mean Square Propagation! Recuerda experimentar con diferentes optimizadores al entrenar modelos, ya que cada uno tiene fortalezas únicas según los datos y la arquitectura. Y si buscas seguir formándote en este y otros temas, nuestra trilogía de fundamentos matemáticos de machine learning te vendrá genial para destacar en la selección de optimizadores clave como el que hemos descubierto en este artículo del blog.