La matriz de confusión es una herramienta útil para supervisar la eficacia de un modelo de clasificación. En este post hablaremos sobre el concepto de matriz de confusión, cómo calcularla y cómo interpretarla.
Hablemos de la matriz de confusión

Qué es una matriz de confusión
Las matrices de confusión son una herramienta muy útil para los científicos y analistas de datos, ya que proporcionan un análisis preciso sobre qué tan bueno es el modelo de clasificación. Estas matrices se utilizan con frecuencia para evaluar los resultados predictivos en machine learning y ciencia de datos, ya sea para propósitos académicos o comerciales.
El análisis mediante matrices de confusión puede ser útil tanto para mejorar las características subyacentes en tus algoritmos de aprendizaje automático para problemas de clasificación, como para probar hipótesis relacionadas con el número total adecuado de observaciones del conjunto de datos usado en el entrenamiento del modelo.
Cómo se calcula una matriz de confusión
Una matriz de confusión se puede calcular usando las predicciones de cada clase del modelo de aprendizaje automático y etiquetar estos resultados como verdaderos positivos, verdaderos negativos, falsos positivos o falsos negativos. El objetivo principal es identificar el número de predicciones correctas, informando así sobre su desempeño en términos precisos y numéricamente expresados.
Para calcular la matriz de confusión, primero hay que identificar los datos de entrada en el algoritmo de clasificación. Estas observaciones de datos deben ser etiquetadas previamente con las clases / categorías correspondientes. Esto significa que hay que saber cuáles son las categorías correctas para cada observación antes del análisis. Después, el modelo puede ejecutarse para predecir las clases / categorías relevantes para cada observación. Estas predicciones se comparan entonces con las etiquetas correctas y se clasifican como verdaderos positivos, verdaderos negativos, falsos positivos o falsos negativos según corresponda. Finalmente, toda esta información se representa en forma tabular en la forma conocida como matriz de confusión.
Cómo calcular una matriz de confusión en Python
Calcular una matriz de confusión en Python requiere de algunos sencillos pasos. Primero, es necesario recopilar datos. Esto incluye crear el conjunto de entrenamiento con las etiquetas correctas para cada observación. Después, el modelo se entrenará y evaluará con los datos obtenidos anteriormente. En tercer lugar, se puede usar la librería Scikit-Learn para calcular la matriz de confusión del modelo predicho. Esta librería contiene diferentes funciones como confusion_matrix() y classification_report(), que se pueden utilizar para generar los resultados de rendimiento del modelo basado en una tabla-matriz y otros valores métricos respectivamente.
Cómo calcular una matriz de confusión para la clasificación multiclase
Hasta ahora hemos estado hablando de matrices de confusión para clasificación binaria. Es decir, solamente con 2 categorías a predecir (positivo y negativo). Calcular una matriz de confusión para la clasificación multiclase requiere tener en cuenta varios aspectos. Primero, es necesario tener en cuenta cada una de las categorías a indicar. En segundo lugar, hay que contar el número de observaciones dentro de cada categoría incluida en el conjunto de datos. Después, hay que calcular el número o porcentaje de aciertos y errores usando los resultados conocidos o reales y los resultados predichos. Finalmente, estos resultados son agrupados para construir la matriz de confusión, es decir, una tabla con los valores predichos versus los reales para cada clase dada. Al igual que en el caso de clasificación binaria, esta matriz puede ser usada como referencia para verificar si un modelo está generalizando bien sus predicciones.
Cómo interpretar la matriz de confusión
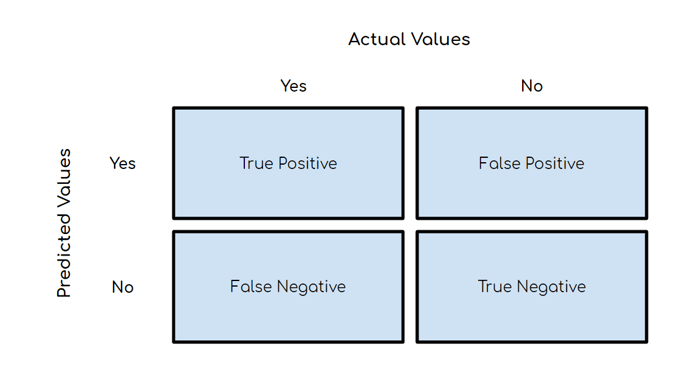
Interpretar una matriz de confusión es importante para cuantificar el rendimiento de un modelo de machine learning. La tabla muestra los resultados de clasificación obtenidos al comparar los valores reales con los predichos por el modelo. Está compuesta por dos filas y dos columnas. Cada columna representa los verdaderos reales y los falsos reales, mientras que cada fila representa los verdaderos predichos y falsos predichos. Esto resulta en 4 celdas que se conocen como verdaderos positivos, falsos positivos, falsos negativos y verdaderos negativos.
Los verdaderos positivos se refieren a aquellas predicciones hechas por un modelo predictivo que son correctas. Esto significa que el modelo ha identificado y etiquetado adecuadamente la clase / categoría para la instancia de datos en cuestión. Los falsos positivos, por otro lado, se refieren a aquellas predicciones que son incorrectas, lo que significa que el modelo no ha podido identificar correctamente la clase / categoría para esa instancia de datos.
Los falsos negativos son aquellas predicciones que etiqueta o clasifica una instancia de datos incorrectamente. Esto se refiere a situaciones en las que el modelo predice que es incorrecto el resultado que es verdadero, lo cual puede resultar en una falta de detección / identificación de los patrones reales y afectar la exactitud del sistema.
Finalmente, los verdaderos negativos se refieren a aquellas predicciones hechas por un modelo predictivo que son correctamente etiquetadas como falsas. Esto significa que el modelo ha identificado y etiquetado correctamente la instancia de datos como no perteneciente a ninguna clase / categoría identificada.
A partir de lo anterior, se puede calcular la tasa de verdaderos positivos (TP) se refiere al número de observaciones con una etiqueta verdadera predicha correctamente. Esto significa que el modelo ha sido capaz de predecir la etiqueta verdadera para ese set de datos. Por otro lado, la tasa de verdaderos negativos (TN) se refiere al número de observaciones con una etiqueta falsa identificada correctamente por el modelo. Esto significa que el modelo ha identificado correctamente las observaciones con un resultado falso. Ambos, tasa de verdaderos positivos y negativos, son importantes para evaluar el rendimiento del modelo y determinar si está cumpliendo con los requerimientos previamente especificados.
Existen varias métricas utilizadas para medir el éxito de una matriz de confusión tales como precisión, sensibilidad / especificidad, F1 score y Mattews Correlation Coefficient (MCC). Estas métricas proporcionan información sobre qué tan bien está funcionando el modelo y también te permiten comparar su desempeño con otros sistemas similares. Es importante entender y cuantificar los errores del modelo, ya que forman parte integral de su rendimiento.
Conclusiones
En resumen, las matrices de confusion son un instrument indispensable para evaluar el rendimiento preciso y numéricamente expresado que ofrece un algoritmo predictivo. Utilizarlas permite mejorar las características subyacentes en dicho algoritmo así como optimizar correctamente el tamaño adecuado del conjunto de datos usado durante el proceso de entrenamiento del modelo y probar hipótesis importantes relacionadas con el mismo.