Las ecuaciones de primer grado son uno de los conceptos fundamentales en matemáticas. Aunque su apariencia puede parecer sencilla, entenderlas correctamente y saber cómo resolverlas es clave para avanzar en álgebra, geometría y muchas aplicaciones prácticas en la vida diaria y en diversas profesiones. En este artículo vamos a explorar qué son las ecuaciones de primer grado, cómo se resuelven paso a paso, ejemplos prácticos y los principales usos que tienen en distintos ámbitos.

1. ¿Qué son las ecuaciones de primer grado?

Una ecuación de primer grado es una igualdad matemática en la que aparece una incógnita (generalmente representada por la letra x) elevada a la potencia 1. Esto significa que la variable no está al cuadrado, al cubo ni con exponentes mayores. Su forma general es:

ax+b=c

donde:

• a, $b$ y $c$ son números reales (a≠0),

• x es la incógnita que queremos despejar.

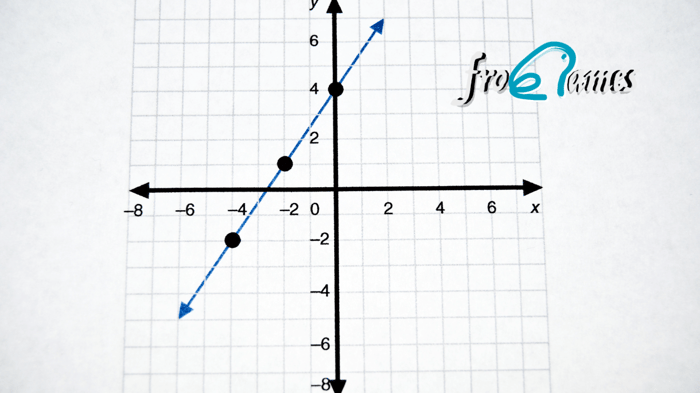
Lo que caracteriza a las ecuaciones de primer grado es precisamente su linealidad: gráficamente, representan una línea recta cuando las representamos en un plano cartesiano. Esto las diferencia de las ecuaciones de segundo grado o superiores, que generan curvas más complejas como parábolas.

2. Elementos de una ecuación de primer grado

Para comprenderlas mejor, es útil identificar los elementos que forman una ecuación de primer grado:

1. Término con incógnita: ax, donde $a$ es el coeficiente.

2. Término independiente: $b$, un número que no tiene incógnita.

3. Igualdad: el signo = que establece que ambos lados tienen el mismo valor.

4. Resultado o constante: c, que puede estar en el lado derecho de la ecuación o trasladarse al izquierdo.

Por ejemplo, en la ecuación:

3x+5=14

• 3x es el término con la incógnita.

• 5 es el término independiente.

• 14 es la constante que iguala la expresión.

3. Cómo resolver ecuaciones de primer grado paso a paso

Resolver una ecuación de primer grado significa encontrar el valor de la incógnita que hace que la igualdad sea verdadera. Los pasos son sistemáticos y se pueden aplicar a cualquier ecuación lineal simple o ligeramente más compleja.

Paso 1: Simplificar términos semejantes

Si hay más de un término con x o varios números, primero hay que sumar o restar términos semejantes dentro de cada lado de la ecuación.

Ejemplo:

2x+3x+7=15

Se suman los coeficientes de x:

5x+7=15

Paso 2: Aislar el término con la incógnita

Trasladamos los términos independientes al otro lado de la ecuación cambiando su signo:

5x=15−7

5x=8

Paso 3: Despejar la incógnita

Dividimos ambos lados de la ecuación por el coeficiente de $x$ para obtener su valor:

x = 8 / 5

Y listo, hemos resuelto la ecuación.

4. Reglas básicas a recordar

Al trabajar con ecuaciones de primer grado, es importante tener en cuenta algunas reglas que permiten resolverlas correctamente:

1. Operar en ambos lados de la ecuación: cualquier operación que hagas en un lado debe hacerse también en el otro. Esto mantiene la igualdad.

2. Sumar o restar números y términos semejantes primero: facilita el aislamiento de la incógnita.

3. Multiplicar o dividir por números distintos de cero: nunca se debe dividir entre cero, ya que es indefinido.

4. Verificar el resultado: sustituye el valor encontrado en la ecuación original para asegurarte de que se cumple la igualdad.

5. Ejemplos prácticos

Veamos algunas ecuaciones de primer grado con distintos niveles de dificultad:

Ejemplo 1: Ecuación sencilla

x+7=12

• Restamos 7 en ambos lados: x=12−7

• Resultado: x=5

Ejemplo 2: Ecuación con coeficiente distinto de 1

4x−3=9

• Sumamos 3: 4x=12

• Dividimos entre 4: x=3

Ejemplo 3: Ecuación con la incógnita en ambos lados

2x+5=x+10

• Restamos $x$ a ambos lados: x+5=10

• Restamos 5: x=5

Ejemplo 4: Ecuación con fracciones

(2 / 3)x + 1 = 5 / 3

• Restamos 1: (2 / 3)x = 5 / 3 − 1 = 2 / 3

• Multiplicamos por 3 / 2: x=1

Estos ejemplos muestran la versatilidad de las ecuaciones de primer grado para distintos escenarios numéricos.

6. Aplicaciones de las ecuaciones de primer grado

Aunque a veces parece un tema abstracto, las ecuaciones de primer grado tienen múltiples aplicaciones en la vida diaria y en diversas disciplinas:

a) Finanzas y economía

Permiten calcular precios, porcentajes, descuentos, intereses y balances.
Ejemplo: Si un producto cuesta x euros y le aplicamos un 20% de descuento quedando en 80 €, podemos plantear:

x − 0, 2x = 80

Resolviendo la ecuación, obtendremos el precio original.

b) Ingeniería y física

Se usan para calcular fuerzas, resistencias, velocidades o distancias cuando la relación es lineal.
Ejemplo: La distancia recorrida $d$ es igual a la velocidad $v$ por el tiempo $t$: $d=vt$. Si conocemos dos de estos valores, podemos plantear una ecuación de primer grado para calcular el tercero.

c) Problemas cotidianos

Desde repartir dinero entre amigos hasta organizar horarios o presupuestos.
Ejemplo: Si tú y tus amigos queréis repartir 120 € entre 4 personas por igual:

x + x + x + x = 120  ⟹  4x = 120  ⟹  x = 30

d) Álgebra y matemáticas avanzadas

Las ecuaciones de primer grado son la base para resolver sistemas de ecuaciones, modelar problemas de optimización y entender funciones lineales.

7. Consejos para dominar las ecuaciones de primer grado

Para mejorar en la resolución de ecuaciones de primer grado, conviene seguir algunas estrategias:

1. Practicar regularmente: cuanto más ejercicios resuelvas, más natural será identificar el tipo de ecuación y los pasos necesarios.

2. Verificar siempre: sustituye el valor de la incógnita en la ecuación original para asegurarte de que es correcto.

3. Aprender a simplificar términos: identifica rápidamente los coeficientes y términos independientes.

4. No temer a los signos negativos y fracciones: son comunes en problemas reales y forman parte de la práctica habitual.

5. Plantear problemas de la vida real: esto ayuda a entender la utilidad y la lógica detrás de las ecuaciones.

8. Resumen

Las ecuaciones de primer grado son un pilar fundamental de las matemáticas. Se caracterizan por tener la incógnita elevada a la potencia 1 y representan relaciones lineales. Resolverlas implica aislar la variable, aplicar operaciones equivalentes a ambos lados y comprobar siempre el resultado.

Se aplican en finanzas, física, ingeniería, problemas cotidianos y como base para estudios matemáticos más avanzados. Dominar las ecuaciones de primer grado no solo ayuda a aprobar exámenes, sino que también desarrolla la lógica, la capacidad de análisis y la resolución de problemas prácticos.

Con práctica, atención a los detalles y comprensión de los pasos básicos, podrás enfrentarte a cualquier ecuación lineal con seguridad. Recuerda que este conocimiento sirve tanto en matemáticas puras como en aplicaciones del día a día.

Aprende sobre Fundamentos del Álgebra con Aprende Matemáticas desde Cero de Frogames Formación

Si te ha interesado lo que te hemos contado en este post, te encantará saber que puedes profundizar en este tema y en todos los conceptos relacionados con los fundamentos del álgebra a través del curso Aprende Matemáticas desde Cero – Fundamentos del Álgebra. Este curso está pensado para quienes quieren empezar desde cero y avanzar con paso firme, aprendiendo de forma sencilla y práctica.

Además, este curso forma parte de la ruta de aprendizaje Aprende Matemáticas desde Cero, una serie de formaciones diseñadas para cubrir diferentes áreas de las matemáticas, desde aritmética hasta álgebra y más allá. Con esta colección, podrás ir construyendo tus conocimientos de manera progresiva y aplicarlos con confianza tanto en estudios como en situaciones cotidianas.

Si quieres dominar los fundamentos matemáticos que sustentan las ecuaciones y otros conceptos esenciales, esta ruta formativa es una opción perfecta para vosotros. ¡No dejéis pasar la oportunidad de aprender y mejorar vuestras habilidades matemáticas!

¡Nos vemos en clase!