Si alguna vez te has sentido perdido al enfrentarte a un eje cartesiano con una función lineal, este artículo es para ti. Aprender a representar gráficamente funciones lineales no solo es fundamental en matemáticas, sino que también sirve como base para entender fenómenos cotidianos, desde economía hasta física. En este post, te guiaré paso a paso para que podáis dibujar cualquier función lineal con seguridad, claridad y sin perder la cabeza en el intento.

1. ¿Qué es una función lineal?

Antes de empezar a dibujar, conviene recordar qué es una función lineal. Una función lineal es aquella que puede expresarse de la forma:

y = mx+b

donde:

• x es la variable independiente.

• y es la variable dependiente.

• m es la pendiente de la recta, que indica la inclinación.

• b es el término independiente o punto de corte con el eje Y.

La característica principal de una función lineal es que su representación gráfica siempre es una línea recta. Esto facilita mucho el proceso, ya que solo necesitas dos puntos bien calculados para dibujarla.

2. Elementos clave para representar gráficamente funciones lineales

Para que la representación sea correcta, hay tres elementos que debes tener en cuenta:

1. Pendiente (m): indica cómo sube o baja la recta.

   • Si m>0, la recta sube hacia la derecha.

   • Si m<0, la recta baja hacia la derecha.

   • Si m=0, la función es constante y la recta es horizontal.

2. Intersección con el eje Y (b): el valor donde la recta cruza el eje vertical. Este es el primer punto que siempre conviene localizar.

3. Puntos adicionales: a partir del punto de intersección y usando la pendiente, puedes calcular al menos otro punto para dibujar la recta con precisión.

3. Paso a paso para representar gráficamente funciones lineales

Vamos a ver un método sistemático para representar gráficamente funciones lineales de manera sencilla.

Paso 1: Identifica la pendiente y el término independiente

Dada la función:

y=2x+3

• La pendiente m=2

• El término independiente b=3

Esto significa que la recta sube 2 unidades por cada 1 unidad que avanzas en x y que cruza el eje Y en el punto (0,3).

Paso 2: Marca el punto de intersección con el eje Y

Localiza b en el eje vertical y marca el punto. En nuestro ejemplo:

(0,3)

Este será tu primer punto de referencia.

Paso 3: Aplica la pendiente para hallar otro punto

La pendiente $m$ se interpreta como "sube / corre".
Para m=2:

• Subida = 2

• Avance en x = 1

A partir de (0,3), sumas 1 en el eje X y 2 en el eje Y:

x = 0+1 = 1, y = 3+2 = 5

Segundo punto: (1,5)

Si la pendiente fuera negativa, restarías en el eje Y en lugar de sumar.

Paso 4: Dibuja la recta

Una vez tengas al menos dos puntos, traza una línea que los conecte. Si queréis mayor precisión, podéis calcular un tercer punto y comprobar que la recta pasa por él. Esto asegura que la gráfica es correcta.

Paso 5: Etiqueta la gráfica

No olvides poner los nombres de los ejes (X y Y) y marcar los valores de los puntos más importantes. Esto hará que la gráfica sea clara y profesional.

4. Ejemplos prácticos de representación

Veamos varios casos para consolidar la técnica de representar gráficamente funciones lineales.

Ejemplo 1: Pendiente positiva

Función:

y = 3x−2

1. m=3, b=−2

2. Punto de intersección: (0, -2)

3. Usando la pendiente: sube 3, avanza 1 → (1,1)

4. Dibuja la recta y verifica un tercer punto: (2,4)

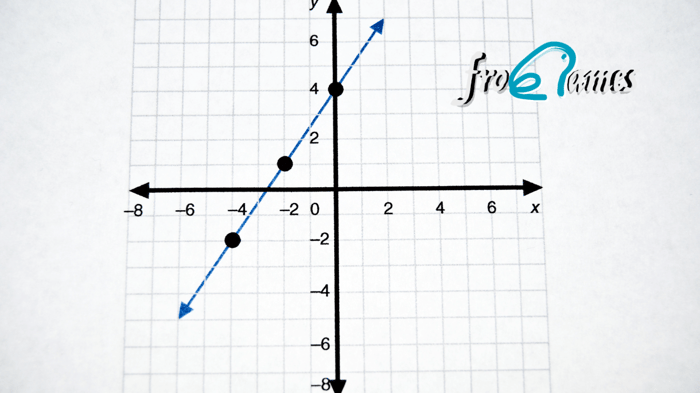
Ejemplo 2: Pendiente negativa

Función:

y = −x+4

1. m=−1, b=4

2. Punto de intersección: (0,4)

3. Pendiente negativa: baja 1, avanza 1 → (1,3)

4. Dibuja la recta, verifica con otro punto: (2,2)

Ejemplo 3: Función horizontal

Función:

y=5

1. Pendiente m=0 → recta horizontal

2. Punto de intersección: (0,5)

3. Segundo punto: cualquier x, y = 5 → (1,5)

4. La gráfica es una línea recta paralela al eje X

Ejemplo 4: Función vertical (no lineal en el sentido estricto)

La ecuación x = 3 no es una función lineal porque no pasa la prueba de la vertical. No obstante, visualmente es útil saberlo: se representa como una línea vertical que cruza el eje X en 3.

5. Consejos para representar funciones lineales más complejas

1. Simplifica la ecuación si es necesario: si la ecuación viene en forma general ax+by+c = 0, despeja y primero:

by=−ax−c ⇒ y = −(a / b)x−c / b

2. Usa una tabla de valores: si la pendiente es fraccionaria, calcular varios puntos ayuda a mantener precisión.

3. Atención a los signos: errores comunes ocurren al sumar o restar términos. Repasa siempre los signos.

4. Revisa el gráfico: sustituye los puntos calculados en la ecuación original para asegurarte de que cumplen la igualdad.

6. Aplicaciones de las funciones lineales

Saber representar gráficamente funciones lineales no es solo útil para aprobar exámenes. Estas funciones aparecen en muchas áreas:

• Economía: costes, ingresos y beneficios lineales.

• Física: relaciones proporcionales entre velocidad y tiempo, fuerza y aceleración.

• Ingeniería: pendientes de rampas, gradientes de presión o temperatura.

• Vida diaria: calcular precios con descuentos o incrementos lineales.

Entender gráficas os permitirá interpretar problemas rápidamente y tomar decisiones informadas.

7. Errores comunes y cómo evitarlos

1. Confundir pendiente con término independiente: recuerda que m controla la inclinación y b el corte con Y.

2. Usar solo un punto: dos puntos son suficientes, pero un tercero ayuda a verificar.

3. No etiquetar los ejes: dificulta la interpretación.

4. Olvidar los signos de la pendiente: afecta la dirección de la recta.

Evitar estos errores os ahorrará frustraciones y tiempo.

8. Recursos y herramientas útiles

Además del método manual, podéis usar herramientas digitales para representar gráficamente funciones lineales:

• GeoGebra: software gratuito y educativo.

• Desmos: plataforma online intuitiva.

• Calculadoras gráficas: muchas permiten dibujar la función introduciendo la ecuación.

Estas herramientas son ideales para comprobar vuestros cálculos y practicar con múltiples funciones.

9. Resumen paso a paso

Para dibujar cualquier función lineal:

1. Identifica pendiente (m) y término independiente (b).

2. Marca el punto de intersección con el eje Y.

3. Usa la pendiente para calcular al menos un punto adicional.

4. Traza la recta que pase por esos puntos.

5. Etiqueta los ejes y verifica los puntos calculados.

Con práctica, este procedimiento se convierte en algo automático y muy útil para cualquier ejercicio o aplicación práctica.

Conclusión

Aprender a representar gráficamente funciones lineales no tiene por qué ser complicado ni aburrido. Conocer la pendiente, el término independiente y aplicar un método paso a paso os permitirá dibujar rectas precisas y comprender cómo se comporta la relación entre variables.

Ya sea en matemáticas puras, física, economía o problemas cotidianos, dominar esta habilidad os dará confianza para analizar y resolver situaciones con rapidez. La clave está en practicar, revisar los cálculos y entender qué representa cada elemento de la ecuación.

Con este conocimiento, estaréis preparados para enfrentar cualquier función lineal que os encuentres, ya sea en el aula, en trabajos prácticos o en la vida real.

Aprende sobre Fundamentos del Álgebra con Aprende Matemáticas desde Cero de Frogames Formación

Si te ha interesado lo que te hemos contado en este post, te encantará saber que puedes profundizar en este tema y en todos los conceptos relacionados con los fundamentos del álgebra a través del curso Aprende Matemáticas desde Cero – Fundamentos del Álgebra. Este curso está pensado para quienes quieren empezar desde cero y avanzar con paso firme, aprendiendo de forma sencilla y práctica.

Además, este curso forma parte de la ruta de aprendizaje Aprende Matemáticas desde Cero, una serie de formaciones diseñadas para cubrir diferentes áreas de las matemáticas, desde aritmética hasta álgebra y más allá. Con esta colección, podrás ir construyendo tus conocimientos de manera progresiva y aplicarlos con confianza tanto en estudios como en situaciones cotidianas.

Si quieres dominar los fundamentos matemáticos que sustentan las ecuaciones y otros conceptos esenciales, esta ruta formativa es una opción perfecta para vosotros. ¡No dejéis pasar la oportunidad de aprender y mejorar vuestras habilidades matemáticas!

¡Nos vemos en clase!