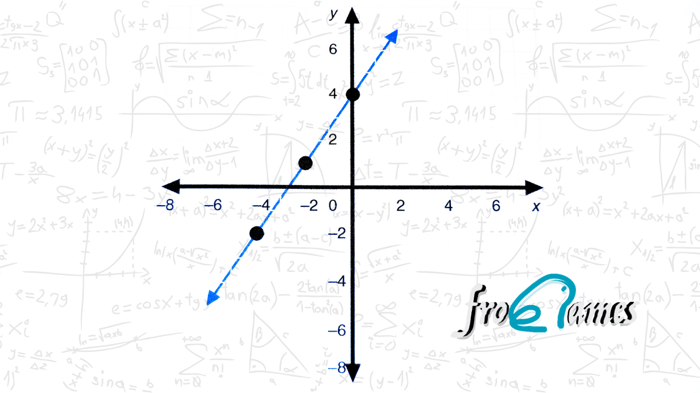
Las matemáticas están mucho más presentes en nuestra vida diaria de lo que solemos imaginar. Una de las herramientas más sencillas y, a la vez, más poderosas en este ámbito es la función lineal. Se trata de una relación matemática entre dos variables que puede expresarse mediante una ecuación de primer grado, del tipo y = m*x + b donde m representa la pendiente y b el punto de corte con el eje vertical. A pesar de su aparente simplicidad, las aplicaciones de la función lineal abarcan un sinfín de contextos en los que se requiere describir relaciones proporcionales o cambios constantes.

En este artículo vamos a explorar con detalle cómo se aplican las funciones lineales en tres campos fundamentales del conocimiento y la práctica profesional: la economía, la física y la ingeniería. Veremos ejemplos concretos, interpretaciones prácticas y la utilidad que tienen para modelizar fenómenos del mundo real.

1. Comprendiendo la función lineal: una base común para distintos campos

Antes de adentrarnos en los ejemplos específicos, conviene repasar brevemente qué caracteriza a una función lineal. En esencia, describe una relación directa y constante entre dos magnitudes. Si una variable aumenta o disminuye en una cantidad determinada, la otra lo hace siempre en la misma proporción.

El valor de la pendiente (m) indica el ritmo del cambio. Por ejemplo, si m = 2, significa que cada vez que la variable xaumenta una unidad, y crece en dos. El término independiente (b) refleja el valor de y cuando x = 0, es decir, el punto de partida o la intersección con el eje vertical.

Gracias a esta estructura tan sencilla, las aplicaciones de la función lineal permiten analizar comportamientos que mantienen una relación estable entre causa y efecto. En otras palabras, son ideales para describir fenómenos donde el cambio es constante.

2. Aplicaciones de la función lineal en economía

En economía, las funciones lineales son una herramienta básica para modelar y entender distintos tipos de relaciones entre variables. La simplicidad de la función lineal facilita la interpretación y la toma de decisiones, especialmente en situaciones donde los factores externos permanecen estables o los cambios son proporcionales.

a) Costes y beneficios

Una de las aplicaciones de la función lineal más comunes en economía se da en el estudio de los costes de producción. Supongamos que una empresa fabrica un producto y que el coste total (C) depende del número de unidades producidas (x). Si los costes fijos son b y el coste por unidad producida es m, la función se expresa como:

C(x) = m*x + b

Aquí, b representa los gastos que la empresa debe asumir aunque no produzca nada (como el alquiler de una nave o los salarios base), mientras que m*x indica el coste variable que depende de la cantidad producida.

De forma análoga, también se pueden modelizar los ingresos y los beneficios:

I(x) = p*x
B(x) = I(x) - C(x)

Si tanto los ingresos como los costes son funciones lineales, el beneficio también lo será.

b) Oferta y demanda

Otro uso clásico es el análisis de la oferta y la demanda. Ambas suelen representarse mediante funciones lineales en un rango limitado. Por ejemplo:

Qd = a - b*P
Qo = c + d*P

donde P es el precio y Q la cantidad. La intersección de ambas rectas indica el punto de equilibrio del mercado, es decir, el precio y la cantidad donde la oferta iguala a la demanda.

Estas representaciones permiten estudiar cómo afectan las variaciones de precios, impuestos o costes de producción al equilibrio económico. Sin duda, este es uno de los ejemplos más didácticos de las aplicaciones de la función lineal en el ámbito económico.

c) Salarios y productividad

También es frecuente usar funciones lineales para estimar relaciones laborales, por ejemplo, entre la productividad y el salario. Si el salario depende directamente de las horas trabajadas o del número de unidades producidas, la relación puede representarse fácilmente con una función de primer grado.

3. Aplicaciones de la función lineal en física

En física, las funciones lineales permiten describir fenómenos en los que una magnitud varía de forma constante respecto a otra. Gracias a ello, se convierten en un recurso esencial para modelizar movimientos, cambios de energía o transformaciones térmicas.

a) Movimiento rectilíneo uniforme

Uno de los ejemplos más claros de aplicaciones de la función lineal en física es el movimiento rectilíneo uniforme (MRU). En este tipo de movimiento, la velocidad es constante, lo que significa que el espacio recorrido (s) depende linealmente del tiempo (t):

s(t) = v*t + s0

Aquí, v es la velocidad constante y s0 la posición inicial. Si representamos esta ecuación en una gráfica, obtenemos una línea recta cuya pendiente es la velocidad.

Este modelo se utiliza para estudiar desplazamientos de vehículos, trayectorias de proyectiles en sus fases iniciales o flujos constantes de partículas, entre otros casos.

b) Ley de Ohm

La ley de Ohm, fundamental en electricidad, es otra manifestación directa de una función lineal. Expresa que la corriente eléctrica (I) que atraviesa un conductor es proporcional al voltaje (V) aplicado, siendo la resistencia (R) la constante de proporcionalidad:

V = R*I

Si representamos V frente a I, obtenemos una línea recta cuya pendiente es la resistencia. Por tanto, la relación entre estas variables es lineal siempre que el material no cambie sus propiedades con la temperatura. Este es un ejemplo clásico en el laboratorio y una de las aplicaciones de la función lineal más recurrentes en física y tecnología.

c) Dilatación térmica

En fenómenos térmicos, muchos materiales se dilatan de forma lineal dentro de un rango de temperaturas. La longitud Lde un cuerpo puede expresarse como:

L = L0*(1 + α*ΔT)

donde L0 es la longitud inicial, α el coeficiente de dilatación lineal y ΔT la variación de temperatura. Aunque no se presenta explícitamente como y = m*x + b, el comportamiento sigue siendo lineal y cumple las mismas propiedades.

4. Aplicaciones de la función lineal en ingeniería

La ingeniería, en todas sus ramas, utiliza la función lineal para modelizar sistemas, planificar proyectos y analizar datos experimentales. Su simplicidad la convierte en una herramienta fundamental tanto para el diseño como para el control.

a) Respuesta de sistemas

En ingeniería eléctrica o mecánica, muchos sistemas pueden aproximarse a un comportamiento lineal dentro de ciertos límites. Por ejemplo, la respuesta de un sensor puede describirse mediante una función lineal que relaciona la señal de salida (y) con la magnitud física medida (x):

y = k*x + c

Esta relación permite calibrar instrumentos y predecir valores con precisión.

b) Planificación y control de proyectos

En ingeniería civil o industrial, también encontramos aplicaciones de la función lineal en la planificación de obras y proyectos. Si se conoce el coste medio por unidad de trabajo, se puede estimar el presupuesto total en función del número de unidades producidas o del tiempo invertido. Lo mismo ocurre con el consumo energético o el uso de materiales.

c) Ensayos y análisis de datos

En ingeniería química, de materiales o mecánica, las funciones lineales se usan constantemente para ajustar datos experimentales. A través de la regresión lineal, se obtiene una recta que aproxima los datos medidos y permite determinar tendencias o relaciones entre variables. Esta técnica es clave para interpretar resultados de laboratorio o validar hipótesis.

5. Por qué las funciones lineales siguen siendo tan útiles

Aunque hoy contamos con herramientas matemáticas mucho más complejas, las aplicaciones de la función lineal siguen siendo imprescindibles. Su gran ventaja es la claridad que ofrecen: permiten predecir resultados, interpretar fenómenos y comunicar ideas con facilidad.

Además, muchas relaciones no lineales pueden aproximarse a una función lineal en rangos limitados, lo que simplifica el análisis sin perder precisión en contextos prácticos. Por eso, tanto en la economía como en la física y la ingeniería, las funciones lineales se emplean como punto de partida para modelos más elaborados. Entre sus principales ventajas destacan:

• Claridad y simplicidad: facilitan la comprensión de las relaciones entre variables.

• Predicción de resultados: permiten estimar valores futuros de manera rápida.

• Interpretación de fenómenos: ayudan a entender cómo interactúan diferentes factores.

• Base para modelos complejos: sirven como punto de partida para aproximaciones y análisis más avanzados.

6. Conclusión

En resumen, las aplicaciones de la función lineal son esenciales en multitud de ámbitos del conocimiento. En economía, permiten entender la relación entre costes, precios o beneficios; en física, describen movimientos, leyes eléctricas y fenómenos térmicos; y en ingeniería, ayudan a modelizar sistemas, planificar recursos y analizar datos.

Lejos de ser un concepto puramente académico, la función lineal es una herramienta viva, práctica y aplicable en el día a día profesional. Su capacidad para representar relaciones proporcionales de forma clara la convierte en una de las bases más sólidas del pensamiento científico y técnico.

Dominar las aplicaciones de la función lineal no solo te permitirá comprender mejor cómo funciona el mundo que te rodea, sino también tomar decisiones más precisas en cualquier ámbito donde la constancia y la proporcionalidad sean clave.

Aprende sobre Fundamentos del Álgebra con Aprende Matemáticas desde Cero de Frogames Formación

Si te ha interesado lo que te hemos contado en este post, te encantará saber que puedes profundizar en este tema y en todos los conceptos relacionados con los fundamentos del álgebra a través del curso Aprende Matemáticas desde Cero – Fundamentos del Álgebra. Este curso está pensado para quienes quieren empezar desde cero y avanzar con paso firme, aprendiendo de forma sencilla y práctica.

Además, este curso forma parte de la ruta de aprendizaje Aprende Matemáticas desde Cero, una serie de formaciones diseñadas para cubrir diferentes áreas de las matemáticas, desde aritmética hasta álgebra y más allá. Con esta colección, podrás ir construyendo tus conocimientos de manera progresiva y aplicarlos con confianza tanto en estudios como en situaciones cotidianas.

Si quieres dominar los fundamentos matemáticos que sustentan las ecuaciones y otros conceptos esenciales, esta ruta formativa es una opción perfecta para vosotros. ¡No dejéis pasar la oportunidad de aprender y mejorar vuestras habilidades matemáticas!

¡Nos vemos en clase!