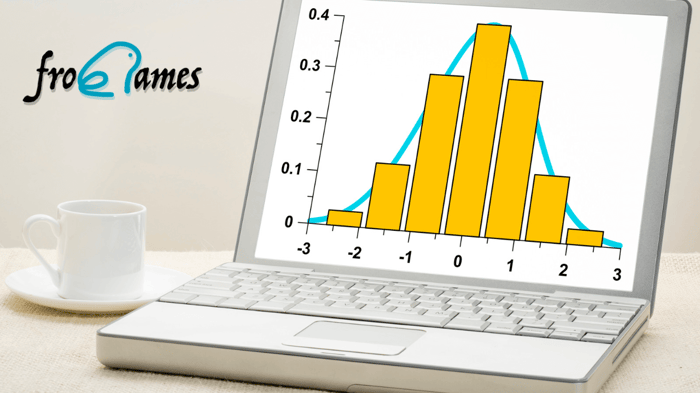
La distribución binomial es un modelo matemático que se utiliza para describir y calcular la probabilidad de eventos binarios (éxito o fracaso) en un conjunto finito de ensayos independientes e idénticamente distribuidos. Se caracteriza por tener dos parámetros: la probabilidad de éxito en cada ensayo y el número total de ensayos. 

Se llama "binomial" porque el resultado de cada ensayo se puede clasificar en dos categorías mutuamente excluyentes (éxito o fracaso). La distribución de probabilidad binomial es ampliamente utilizada en la estadística y en otros campos para modelar y predecir eventos aleatorios.

La binomial es una de las distribuciones de probabilidad más importantes en la estadística y en otros campos que involucran eventos aleatorios. Algunas de las razones por las que es tan importante son:

1. Modelado de eventos binarios: La distribución de probabilidad binomial es el modelo ideal para describir eventos binarios, es decir, eventos que tienen solo dos posibles resultados (éxito o fracaso). Ejemplos de eventos binarios incluyen el resultado de un experimento de laboratorio, el lanzamiento de una moneda o el éxito o fracaso de una campaña publicitaria.

2. Cálculo de probabilidades: Esta distribución permite calcular la probabilidad de que ocurran ciertos eventos en un conjunto finito de ensayos. Por ejemplo, se puede utilizar para calcular la probabilidad de que se obtengan exactamente dos caras en tres lanzamientos de una moneda justa (existe la misma probabilidad de sacar cara que cruz).

3. Toma de decisiones: La distribución binomial se utiliza para ayudar a tomar decisiones basadas en eventos aleatorios. Por ejemplo, una empresa podría utilizar esta distribución para decidir si lanzar una campaña publicitaria basada en la probabilidad de éxito y fracaso.

4. Estimación de parámetros: La binomial también se utiliza para estimar la probabilidad de éxito en un conjunto finito de ensayos. Esto puede ser útil para predecir la probabilidad de éxito en experimentos futuros.

5. Relación con otras distribuciones estadísticas: La distribución de probabilidad binomial es un caso especial de la distribución hipergeométrica y la distribución de Poisson, lo que significa que la binomial está relacionada con otras distribuciones estadísticas y puede ser utilizada en conjunto con ellas para analizar eventos aleatorios más complejos.

Conceptos clave

Cuando hablamos de la distribución binomial, es importante conocer los conceptos clave mostrados a continuación:

1. Experimento binomial: La distribución de probabilidad binomial se aplica a experimentos que cumplen con ciertas condiciones. Estas condiciones son que cada ensayo tiene solo dos posibles resultados, que se consideran "éxito" o "fracaso", y que los ensayos son independientes entre sí.

2. Ensayos independientes e idénticamente distribuidos: Los ensayos de un experimento binomial son independientes entre sí, lo que significa que el resultado de un ensayo no afecta al resultado de los demás ensayos. Además, los ensayos son idénticamente distribuidos, lo que significa que la probabilidad de éxito y fracaso es constante para cada ensayo.

3. Probabilidad de éxito y fracaso en cada ensayo: Cada ensayo del experimento binomial tiene una probabilidad de éxito (p) y una probabilidad de fracaso (q), que es igual a 1-p. La suma de estas dos probabilidades es igual a 1.

4. Número total de ensayos y eventos de interés: El número total de ensayos en el experimento binomial se representa por la letra n. El número de eventos de interés, es decir, el número de éxitos que se esperan en los n ensayos, se representa por la letra x.

5. Función de probabilidad binomial: La función de probabilidad binomial describe la probabilidad de que ocurran exactamente x éxitos en n ensayos del experimento binomial. La fórmula de la función de probabilidad binomial es
   

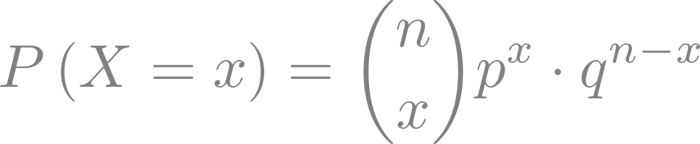
Estos conceptos son esenciales para comprender y calcular la distribución binomial.

Cálculo de la distribución binomial

Como hemos dicho en el apartado anterior, la fórmula matemática para calcular la distribución de probabilidad binomial es la siguiente:

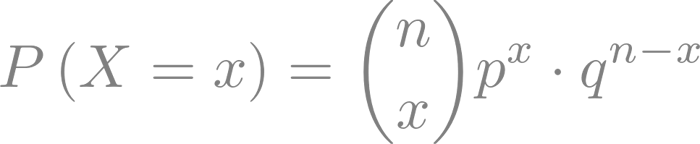
Donde:

• P(X = x) es la probabilidad de que ocurran exactamente x éxitos en n ensayos.
• X es la variable aleatoria que sigue una binomial B(n, p).
• x es el número de éxitos.
• n es el número total de ensayos.
• p es la probabilidad de éxito en cada ensayo.
• q es la probabilidad de fracaso en cada ensayo, que es igual a 1-p.
• El número combinatorio de n sobre x es el coeficiente binomial que se utiliza para calcular el número de combinaciones posibles de x éxitos en n ensayos.

A continuación, veamos un ejemplo de cálculo de la distribución de probabilidad binomial con datos hipotéticos:

Supongamos que se está llevando a cabo un experimento en el que se lanza una moneda justa 5 veces. Queremos saber cuál es la probabilidad de obtener exactamente 3 caras en los 5 lanzamientos.

• En este caso, n = 5, ya que se están realizando 5 lanzamientos de la moneda.
• La probabilidad de éxito en cada lanzamiento es p = 0.5, ya que se trata de una moneda justa y la probabilidad de obtener cara o cruz es la misma.
• La probabilidad de fracaso en cada lanzamiento es q = 0.5, ya que es igual a 1-p.
• Para calcular el número de combinaciones posibles de 3 éxitos en 5 ensayos, se utiliza el coeficiente binomial. En este caso, el número combinatorio de 5 sobre 3 es 10, que se calcula de la siguiente manera:

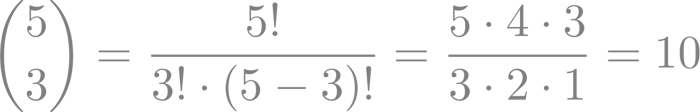
• Sustituyendo los valores en la fórmula, obtenemos:

P(X = 3) = 10 · 0.5^3 · 0.5^(5-3) = 10 · 0.125 · 0.25 = 0.3125

Por lo tanto, la probabilidad de obtener exactamente 3 caras en 5 lanzamientos de una moneda justa es 0.3125.

Propiedades

Las principales propiedades de la distribución de probabilidad binomial son las siguientes:

1. Distribución discreta: La binomial es una distribución de probabilidad discreta, ya que se utiliza para modelar eventos que tienen resultados discretos, como éxitos o fracasos.

2. Distribución de probabilidad: La binomial es una distribución de probabilidad, lo que significa que describe la probabilidad de que ocurran diferentes resultados en un experimento binomial.

3. Función de probabilidad: La función de probabilidad binomial se utiliza para calcular la probabilidad de que ocurran exactamente x éxitos en n ensayos.

4. Simetría: Si la probabilidad de éxito es igual a la probabilidad de fracaso (p = q), entonces la distribución de probabilidad binomial es simétrica. En este caso, la media y la mediana de la distribución son iguales.

5. Media y desviación estándar: La media de la binomial es igual a np, donde n es el número total de ensayos y p es la probabilidad de éxito en cada ensayo. La desviación estándar de esta distribución es igual a sqrt(npq), donde q es la probabilidad de fracaso en cada ensayo.

6. Teorema del límite central: El teorema del límite central establece que la distribución de probabilidad binomial se aproxima a una distribución normal cuando el número de ensayos n es grande.

7. Independencia: Los ensayos de un experimento binomial son independientes entre sí, lo que significa que el resultado de un ensayo no afecta al resultado de los demás ensayos.

Estas propiedades son esenciales para comprender y utilizar la distribución de probabilidad binomial en aplicaciones prácticas.

Aplicaciones

La distribución binomial se utiliza comúnmente en una variedad de situaciones del mundo real, incluyendo:

1. Éxito o fracaso en un negocio: La binomial se puede usar para modelar la probabilidad de que un negocio tenga éxito o fracase. Por ejemplo, si se sabe que la tasa de éxito de los negocios en un área determinada es del 60%, se puede utilizar esta distribución de probabilidad para calcular la probabilidad de que un nuevo negocio tenga éxito en ese área.

2. Probabilidades de eventos deportivos: Se puede modelar la probabilidad de que un equipo gane o pierda un partido en función de la tasa de éxito del equipo y el número de partidos jugados. Por ejemplo, si un equipo tiene una tasa de éxito del 70% y jugará 10 partidos, se puede utilizar la binomial para calcular la probabilidad de que el equipo gane exactamente 7 partidos.

3. Pruebas médicas: La binomial se puede usar para modelar la probabilidad de resultados positivos o negativos en pruebas médicas. Por ejemplo, si una prueba de detección de una enfermedad tiene una tasa de acierto del 95%, se puede calcular la probabilidad de que un paciente tenga un resultado falso positivo o falso negativo con esta distribución.

4. Fabricación de productos: La distribución binomial se puede usar para modelar la probabilidad de que un producto sea defectuoso o no. Por ejemplo, si una línea de producción de una fábrica produce productos defectuosos con una tasa del 5%, se puede calcular la probabilidad de que se produzcan 3 productos defectuosos en un lote de 50.

En resumen, la distribución de probabilidad binomial se utiliza en situaciones del mundo real donde hay dos resultados posibles, como éxito o fracaso, positivo o negativo, ganar o perder. 

Relación con otras distribuciones estadísticas

La distribución binomial está relacionada con otras distribuciones estadísticas, tales como:

1. Distribución de Bernoulli: La distribución de Bernoulli es un caso especial de la distribución binomial, en la cual solo hay un ensayo (n = 1). Es decir, la distribución de Bernoulli se utiliza para modelar la probabilidad de éxito o fracaso en un solo experimento, mientras que la distribución binomial se utiliza para modelar la probabilidad de un número fijo de éxitos en un número fijo de ensayos.

2. Distribución Poisson: La distribución Poisson se utiliza para modelar el número de ocurrencias de un evento raro en un intervalo de tiempo o espacio fijo, mientras que la distribución binomial se utiliza para modelar el número de éxitos en un número fijo de ensayos independientes y con reemplazo. Si el número de ensayos es grande (n grande) y la probabilidad de éxito es pequeña (p pequeña), entonces la distribución binomial se puede aproximar a la distribución Poisson.

3. Distribución normal: La distribución normal se utiliza para modelar muchos fenómenos naturales, y es especialmente útil para modelar distribuciones continuas. En el caso de la distribución binomial, si el número de ensayos es grande (n grande) y la probabilidad de éxito no es demasiado cercana a 0 o 1, entonces la distribución binomial se puede aproximar a la distribución normal. Esto se conoce como el teorema del límite central, y permite utilizar las propiedades de la distribución normal para aproximar la distribución binomial.

Estas relaciones son importantes para comprender las propiedades y aplicaciones de la distribución binomial en la estadística.

Softwares para trabajar con la distribución binomial

Existen varios programas de software estadístico que permiten calcular y graficar la distribución binomial de manera rápida y precisa. Algunos de los más populares son:

1. R: R es un lenguaje de programación estadístico gratuito y de código abierto. Para calcular la distribución binomial en R, se puede utilizar la función dbinom(). Por ejemplo, para calcular la probabilidad de obtener 3 éxitos en 5 ensayos con una probabilidad de éxito del 50%, se puede escribir dbinom(3, 5, 0.5). Para graficar la distribución binomial, se puede utilizar la función plot() con el resultado de la función dbinom().

2. Python: Python es un lenguaje de programación generalista que también cuenta con librerías estadísticas. Para calcular la distribución binomial en Python, se puede utilizar la función scipy.stats.binom.pmf(). Por ejemplo, para calcular la probabilidad de obtener 3 éxitos en 5 ensayos con una probabilidad de éxito del 50%, se puede escribir scipy.stats.binom.pmf(3, 5, 0.5). Para graficar la distribución binomial, se puede utilizar la librería matplotlib.

3. Excel: Excel es una herramienta ampliamente utilizada para realizar cálculos estadísticos y gráficos. Para calcular la distribución binomial en Excel, se puede utilizar la función BINOM.DIST(). Por ejemplo, para calcular la probabilidad de obtener 3 éxitos en 5 ensayos con una probabilidad de éxito del 50%, se puede escribir BINOM.DIST(3, 5, 0.5, FALSE). Para graficar la distribución binomial, se puede utilizar la función Gráfico de dispersión (scatter chart) en Excel.

En el curso "Probabilidad para Machine Learning y Big Data con R y Python" de Frogames, puedes aprender sobre la distribución binomial y otras distribuciones estadísticas importantes. A través de lecciones teóricas y prácticas, aprenderás a aplicar estas distribuciones en el análisis de datos y en la toma de decisiones. Además, el curso te enseñará a utilizar R y Python para realizar cálculos y gráficos de distribuciones estadísticas, incluyendo la distribución binomial. Con este conocimiento, estarás mejor preparado para trabajar en proyectos de análisis de datos y en la implementación de algoritmos de Machine Learning y Big Data.

Conclusiones

En conclusión, la distribución binomial es una herramienta importante en la estadística y en muchos campos de aplicación. Comprender y aplicar la distribución de probabilidad binomial puede ayudar a los tomadores de decisiones a tomar decisiones más informadas y a los investigadores a analizar los resultados de los experimentos de manera más precisa. Además, la distribución binomial se utiliza a menudo en el control de calidad y en el análisis de encuestas.

En la toma de decisiones, la distribución binomial puede ayudar a evaluar las probabilidades de éxito o fracaso en un negocio, la probabilidad de ganar en un evento deportivo o la probabilidad de que un tratamiento médico sea efectivo. En la investigación científica, la distribución binomial se utiliza para analizar los resultados de los experimentos y determinar la probabilidad de que un evento específico ocurra.

En resumen, la distribución binomial es una herramienta fundamental en la estadística y en muchos campos de aplicación. Su comprensión y aplicación son esenciales para tomar decisiones informadas y para la investigación científica rigurosa.