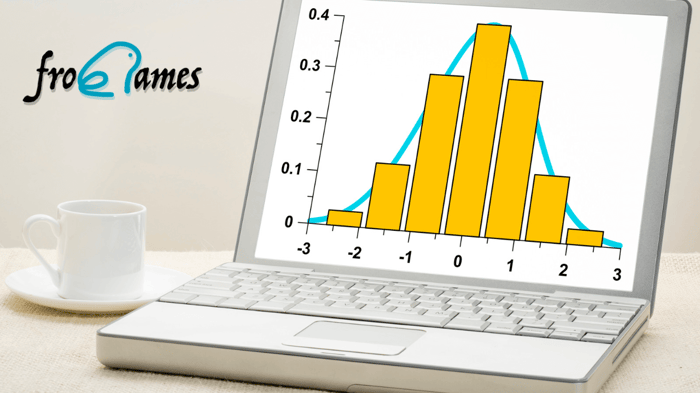
La distribución normal, también conocida como distribución de Gauss o campana de Gauss, es una de las distribuciones de probabilidad más importantes y utilizadas en estadística. Ésta describe la distribución de una variable aleatoria continua en una población.

La forma de la distribución normal es simétrica y en forma de campana, con la mayoría de los valores cercanos a la media o valor central y menos valores extremos a medida que éstos se alejan de la media. Por tanto, los valores más comunes se encuentran en el centro de la distribución y disminuyen gradualmente hacia los extremos.

La distribución normal y su importancia en estadística

La distribución normal es importante en estadística porque muchos fenómenos naturales, como la altura o el peso de una población, tienden a seguir esta distribución. Además, se utiliza ampliamente en pruebas de hipótesis, estimación de intervalos de confianza y modelado estadístico.

La distribución normal tiene dos parámetros: la media y la desviación estándar. La media determina la posición central de la campana, mientras que la desviación estándar indica qué tan amplia es la campana. La fórmula matemática para la distribución normal es:

Donde x es el valor de la variable aleatoria, μ es la media y σ es la desviación estándar.

Características de la distribución normal 

La distribución normal tiene varias características que la hacen única y útil en una variedad de situaciones.

Una de las características más destacadas de la distribución normal es su simetría. La curva de la distribución es simétrica en torno a su media, lo que significa que la mitad de los valores están por encima de la media y la otra mitad están por debajo de ella. Además, la curva es unimodal, es decir, tiene un solo pico.

Otra característica importante es su forma de campana. Los valores en la cola de la distribución son menos probables que los valores cercanos a la media. La curva tiene una altura máxima en la media y disminuye gradualmente en ambas direcciones.

La distribución normal se define por dos parámetros: la media (μ) y la desviación típica (σ). La media es el valor central de la distribución y se encuentra en el punto donde la curva alcanza su altura máxima. La desviación estándar es una medida de la variabilidad de la distribución y mide cuánto se alejan los valores de la media. En la distribución normal, el 68% de los valores se encuentran dentro de una desviación típica de la media y el 95% de los valores se encuentran dentro de dos desviaciones estándar de la media.

Estas características hacen que la distribución normal sea útil para modelar muchos fenómenos naturales, sociales y económicos. Por ejemplo, se puede utilizar para modelar la altura de las personas, los puntajes en un examen o la duración de las llamadas telefónicas, entre otros. Además, muchas pruebas estadísticas se basan en suposiciones sobre la distribución normal de los datos, lo que hace que sea importante comprender y utilizar correctamente esta distribución.

Cálculos con la distribución normal

La distribución normal es importante en estadística porque muchos fenómenos naturales y sociales pueden ser aproximados por esta distribución, también conocida como la curva normal o la curva en forma de campana. Los cálculos que se pueden realizar con la distribución normal incluyen:

1. Cálculo de probabilidades: Dado un valor x, podemos calcular la probabilidad de que un valor aleatorio de la distribución normal sea menor o igual a x. Esto se hace mediante la función de distribución acumulativa (CDF) de la distribución normal.

2. Z-score: El z-score es una medida de a cuántas desviaciones estándar está un valor x de la media μ. El z-score se calcula como (x-μ)/σ.

3. Tabla de distribución normal: Una tabla de distribución normal proporciona los valores de la función de distribución acumulativa (CDF) para diferentes valores de z. Esto hace que sea fácil calcular probabilidades de la distribución normal.

4. Cálculo de percentiles: El percentil p de la distribución normal es el valor x tal que la probabilidad de que un valor aleatorio sea menor o igual a x es igual a p. Los percentiles se pueden calcular utilizando la tabla de distribución normal o mediante fórmulas.

5. Transformación de variables: Si los datos no siguen una distribución normal, se pueden transformar para que sí lo hagan. Por ejemplo, la transformación logarítmica es una transformación común para hacer que los datos se ajusten a una distribución normal. Esto se puede hacer antes de realizar análisis estadísticos para asegurarse de que los supuestos de normalidad se cumplan.

Aplicaciones de la distribución normal

La distribución normal es una de las herramientas estadísticas más importantes que se utilizan en una amplia variedad de campos. A continuación, describimos algunas de las aplicaciones más comunes de esta distribución:

1. Análisis de datos: La distribución normal se utiliza para describir la forma en que se distribuyen los datos en una muestra o población, lo que permite a los analistas realizar una amplia variedad de análisis estadísticos.

2. Contraste de hipótesis: La distribución normal se utiliza en pruebas de contraste de hipótesis para evaluar la probabilidad de que una observación o un conjunto de observaciones provenga de una población con una media y una desviación típica conocidas.

3. Intervalos de confianza: Los intervalos de confianza se utilizan para estimar la probabilidad de que la verdadera media de una población esté dentro de un intervalo específico. La distribución normal se utiliza para calcular los límites del intervalo de confianza.

4. Vida cotidiana: La distribución normal se utiliza en una variedad de situaciones cotidianas, como en el diseño de productos para garantizar que sean seguros y confiables, o para evaluar el desempeño de los estudiantes en un examen.

5. Economía y finanzas: La distribución normal se utiliza para modelar y analizar los rendimientos de las inversiones y otros datos financieros.

6. Ciencias naturales: La distribución normal se utiliza para modelar una amplia variedad de fenómenos en las ciencias naturales, como la altura de las personas, el peso de los animales, la concentración de contaminantes en el aire y el agua, y la duración de las tormentas.

7. Ingeniería y tecnología: La distribución normal se utiliza en el diseño y la evaluación de productos y sistemas en una amplia variedad de campos, como la ingeniería mecánica, la ingeniería eléctrica, la ingeniería de software y la tecnología de la información.

En conclusión, la distribución normal es una herramienta fundamental en el análisis estadístico y se utiliza en diversos campos como el análisis de datos, la prueba de hipótesis, la construcción de intervalos de confianza y muchas otras aplicaciones. Además, la distribución normal tiene una presencia significativa en la vida cotidiana, en la economía y finanzas, en ciencias naturales y en ingeniería y tecnología.

Es importante entender la distribución normal y cómo se aplica en diferentes contextos para poder tomar decisiones informadas y obtener conclusiones precisas a partir de los datos. Por lo tanto, recomendamos profundizar en el tema y explorar más a fondo su aplicación en diferentes áreas.

En resumen, la distribución normal es una herramienta poderosa en el análisis estadístico y su comprensión es esencial para aquellos que buscan tomar decisiones informadas basadas en datos precisos.

Recursos adicionales

En Frogames Formación, ofrecemos una variedad de cursos de estadística que incluyen Estadística Descriptiva y Estadística Inferencial. En estos cursos, se estudian conceptos fundamentales como la distribución normal, junto con muchas otras técnicas importantes en el mundo de la estadística. 

Al aprender sobre la distribución normal y otras herramientas estadísticas, los estudiantes pueden adquirir habilidades valiosas para analizar datos y tomar decisiones informadas en sus carreras y en la vida cotidiana. Además, los estudiantes que deseen profundizar en el tema pueden continuar su aprendizaje en cursos avanzados de la ruta de matemáticas y aplicar estas habilidades en campos como la economía, las finanzas, la ciencia, la tecnología y muchos otros. ¡Únete a Frogames Formación y da el primer paso en tu viaje de aprendizaje en estadística hoy mismo!