Los logaritmos son un proceso fundamental en matemáticas que ha influido en campos tan diversos como la ciencia, la ingeniería y la economía. Aunque su nombre puede sonar intimidante, en realidad son una herramienta poderosa que simplifica problemas y revela patrones subyacentes en una variedad de situaciones. En este post, exploraremos el fascinante mundo de los logaritmos, desde su definición e historia hasta sus aplicaciones prácticas en el mundo real.

De multiplicaciones a sumas: descifrando el mundo de los logaritmos

¿Qué son los logaritmos y por qué son importantes?

Los logaritmos son una función matemática que nos ayuda a resolver problemas relacionados con el crecimiento, el decrecimiento, las tasas y las proporciones. La función logarítmica es la inversa de la función exponencial y nos permite responder preguntas como "¿cuántas veces tengo que multiplicar un número por sí mismo para obtener otro número?".

La definición de logaritmo es la siguiente: el logaritmo en base a de un número real positivo b es el exponente c de a para obtener b.

Un poco de historia sobre los logaritmos

Imagina vivir en una época sin calculadoras ni ordenadores. Resolver cálculos matemáticos complejos era todo un desafío. Pero en el siglo XVI, un matemático escocés llamado John Napier tuvo una idea genial. Se dio cuenta de que podía simplificar las multiplicaciones y divisiones usando lo que llamó "números artificiales". Estos números permitían convertir estas operaciones en sumas y restas más manejables.

Años después, en el siglo XVII, otro matemático inglés llamado Henry Briggs se unió al juego. Él trabajó en colaboración con Napier y refinó la idea. En lugar de usar números artificiales, decidieron usar logaritmos. Estos logaritmos permitían convertir multiplicaciones en sumas y divisiones en restas, lo que hacía que los cálculos fueran mucho más fáciles.

Briggs fue un verdadero pionero al crear tablas de logaritmos, que eran como guías matemáticas antes de que existieran las calculadoras. Las personas podían buscar en estas tablas los logaritmos de diferentes números para facilitar sus cálculos. Fue un gran avance en una época en la que los cálculos eran una tarea larga y tediosa.

Con el tiempo, los logaritmos se volvieron esenciales en astronomía, navegación, matemáticas y muchas otras áreas. Ayudaron a los científicos a realizar cálculos más rápido y a comprender mejor el mundo que los rodeaba.

Hoy en día, aunque tenemos calculadoras y ordenadores potentes, los logaritmos siguen siendo una herramienta poderosa en matemáticas y en campos como la ciencia de datos y la ingeniería. 

Propiedades y reglas de los logaritmos

Una de las razones por las que los logaritmos son tan útiles es debido a sus propiedades y reglas. Algunas de las reglas básicas incluyen la regla de la multiplicación, la regla de la división y la regla del cambio de base. Estas reglas nos permiten simplificar ecuaciones y resolver problemas complejos de manera más rápida y precisa.

Regla de la multiplicación

La suma de logaritmos de la misma base es el logaritmo del producto:

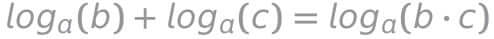
Regla de la división

La resta de logaritmos de la misma base es el logaritmo de la división:

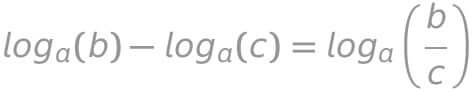
Regla del cambio de base

A continuación, mostramos la fórmula de la regla del cambio de base:

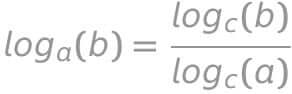
Aplicaciones en el mundo real

Los logaritmos, a pesar de su aparente complejidad, tienen aplicaciones sorprendentemente prácticas en el mundo real. Estas aplicaciones se extienden desde la ciencia hasta la tecnología y la economía, demostrando su importancia en una variedad de contextos. Aquí hay algunas áreas donde los logaritmos desempeñan un papel crucial:

Finanzas y economía

En el cálculo de tasas de interés compuesto, los logaritmos se utilizan para determinar el tiempo necesario para duplicar una inversión. Además, son fundamentales en la modelización de crecimiento económico y en la determinación de tasas de inflación.

Biología y medicina

En estos campos, los logaritmos son utilizados para modelar el crecimiento y la descomposición de sustancias. Por ejemplo, en farmacocinética, los logaritmos son empleados para analizar la absorción y eliminación de medicamentos en el cuerpo humano. También se aplican en la determinación de la concentración de sustancias en análisis químicos y médicos.

Física

Los logaritmos tienen un papel crucial en la física, especialmente en el estudio de fenómenos que involucran crecimiento o decrecimiento exponencial. Por ejemplo, en la radioactividad, los logaritmos se utilizan para calcular la vida media de un isótopo. También son esenciales en la teoría de circuitos eléctricos y en el análisis de señales en la ingeniería electrónica.

Geología y paleontología

En geología, los logaritmos se aplican para calcular el tiempo que ha transcurrido desde eventos geológicos, como la formación de rocas o fósiles. También son útiles en la datación por radiocarbono, que se basa en el decrecimiento exponencial de los isótopos radiactivos.

Estadística y análisis de datos

Aquí, los logaritmos ayudan a transformar datos para que sigan distribuciones normales o para que la relación entre variables sea más clara. Esto es especialmente útil en la representación gráfica de datos que varían en orden de magnitud.

Logaritmos en la era digital

En la era de la tecnología digital, los logaritmos también juegan un papel crucial. Los algoritmos de compresión, como el algoritmo ZIP, se basan en los logaritmos para reducir el tamaño de archivos. Además, el concepto de complejidad algorítmica y Big O notation se relaciona con los logaritmos y su capacidad para medir la eficiencia de los algoritmos.

El futuro de los logaritmos

A medida que avanzamos en la era de la inteligencia artificial y el análisis de datos, los logaritmos siguen siendo relevantes. Son una parte esencial de la estadística y el análisis numérico, permitiendo a los data scientists modelar y comprender patrones en grandes conjuntos de datos.

En definitiva, los logaritmos son una herramienta matemática poderosa que ha influido en innumerables aspectos de nuestra vida y en diversas disciplinas. Desde su origen histórico hasta sus aplicaciones modernas, los logaritmos continúan sorprendiéndonos con su versatilidad y utilidad en la resolución de problemas complejos. Al entender los logaritmos, nos damos cuenta de que las matemáticas no solo son abstracciones teóricas, sino herramientas prácticas que moldean nuestro mundo de maneras sorprendentes y significativas.