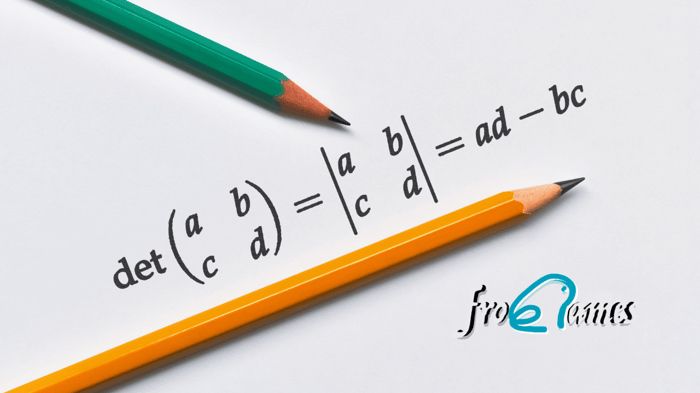Las matrices son una poderosa herramienta matemática que se encuentra en el corazón de muchas disciplinas y aplicaciones en la vida cotidiana. 

Desde el análisis de datos hasta la resolución de problemas en ingeniería y física, la matriz es una herramienta fundamental que nos permite organizar y manipular información de manera eficiente. 

En este post de blog, exploraremos qué son las matrices, cómo operar con ellas y cómo se aplican en diferentes campos, brindándote una comprensión completa de su importancia en el mundo moderno.

Introducción

En matemáticas, una matriz es una estructura rectangular compuesta por filas y columnas que contiene elementos dispuestos de manera ordenada en una cuadrícula. Una matriz se denota con una letra mayúscula, y sus elementos se representan por medio de letras minúsculas acompañadas de dos subíndices que indican su posición en la matriz. 

Por ejemplo, si A es una matriz, sus elementos se representarán como a_ij, donde "i" corresponde a la fila y "j" a la columna.

A continuación tenemos un ejemplo de matriz:

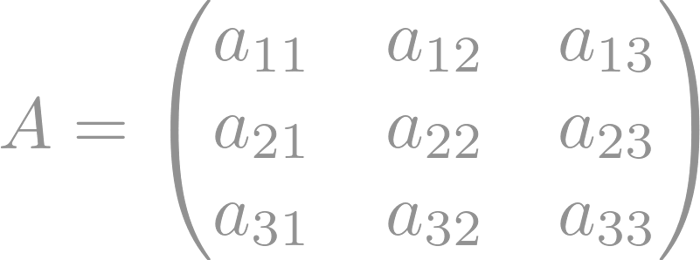
En este ejemplo, A es una matriz de 3x3, ya que tiene 3 filas y 3 columnas. Los elementos a_ij representan los valores contenidos en la fila i y columna j.

Operaciones básicas

Suma y Resta

La suma y resta se realizan entre matrices de la misma dimensión, es decir, matrices que tienen la misma cantidad de filas y columnas.

Para sumar la matriz A y la matriz B, ambas con la misma dimensión, simplemente sumamos los elementos correspondientes de ambas matrices y creamos una nueva matriz resultante. La suma se realiza elemento a elemento.

Veamos un ejemplo: dadas A y B,

La suma A + B es:

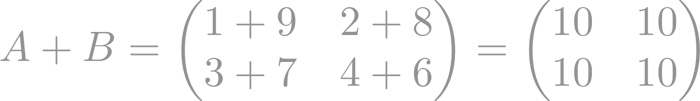
La resta también se realiza elemento a elemento, similar a la suma. Restamos los elementos correspondientes de ambas matrices para obtener una nueva matriz resultante.

Considerando las matrices A y B del ejemplo anterior, la resta A - B es:

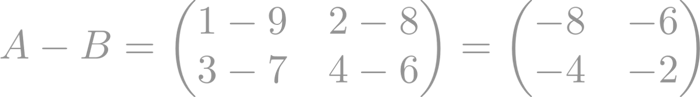
Multiplicación de una Matriz por un Escalar

La multiplicación de una matriz por un escalar (un número) es una operación que consiste en multiplicar cada elemento de la matriz por ese número.

Considerando la matriz A del ejemplo anterior y el escalar c = 2, la multiplicación de la matriz A por el escalar c, que se corresponde con c * A, es:

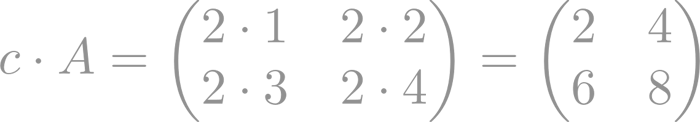
Producto

El producto de dos matrices A y B es una operación más compleja y se puede realizar solamente si el número de columnas de la matriz A es igual al número de filas de la matriz B.

El producto de una matriz A de dimensión m x n y una matriz B de dimensión n x p resulta en una matriz C de dimensión m x p.

El elemento en la fila i y columna j de la matriz resultante C se obtiene multiplicando los elementos correspondientes de la fila i de A con la columna j de B, y sumando esos productos.

Veamos un ejemplo: dadas A y B,

El producto A * B es: 

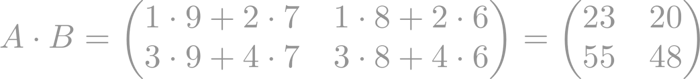
Es importante notar que el producto no es conmutativo. Es decir, en general, A * B no es igual a B * A. Además, no todas las combinaciones de matrices permiten un producto válido. Solo es posible calcular el producto A * B cuando el número de columnas de A coincide con el número de filas de B.

Tipos especiales de matrices

Matriz identidad y su papel en las operaciones matriciales

La matriz identidad es una matriz cuadrada (mismo número de filas que de columnas) que tiene unos (1) en su diagonal principal y ceros (0) en el resto de sus elementos. Se denota comúnmente como "I" o "I_n", donde "n" representa la dimensión de la matriz cuadrada (n x n).

La matriz identidad 3x3 es

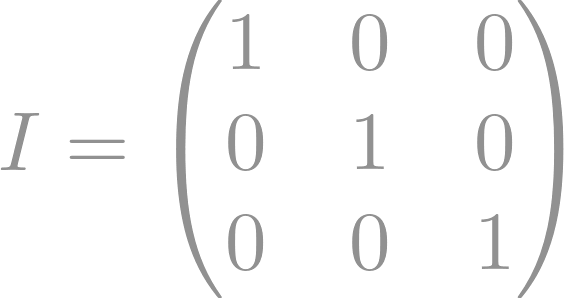
La matriz identidad tiene un papel fundamental en las operaciones matriciales, similar al número 1 en las operaciones con números reales. Cuando multiplicamos cualquier matriz A por la matriz identidad I, el resultado es la misma matriz A. En otras palabras, la matriz identidad actúa como el "elemento neutro" del producto de matrices.

Matriz diagonal, triangular superior y triangular inferior

Se dice que una matriz es diagonal cuando es  cuadrada y todos los elementos fuera de la diagonal principal son cero. Los elementos en la diagonal principal pueden ser cero o cualquier otro valor.

A continuación mostramos un ejemplo de matriz diagonal:

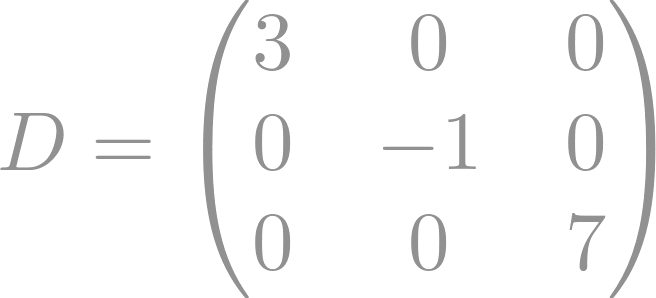
Este tipo de matriz, la matriz diagonal, es útil en diversas aplicaciones, como la resolución de sistemas de ecuaciones lineales, donde pueden simplificar los cálculos enormemente.

Por otro lado, las matrices triangulares son matrices cuadradas en las cuales todos los elementos por encima o por debajo de la diagonal principal son cero.

Existe la matriz triangular superior, donde todos los elementos por debajo de la diagonal principal son cero:

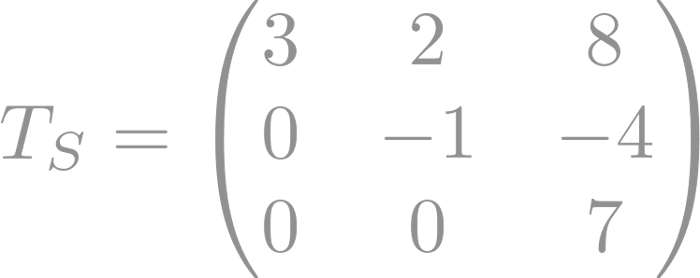
Y luego, la matriz triangular inferior, donde todos los elementos por encima de la diagonal principal son cero:

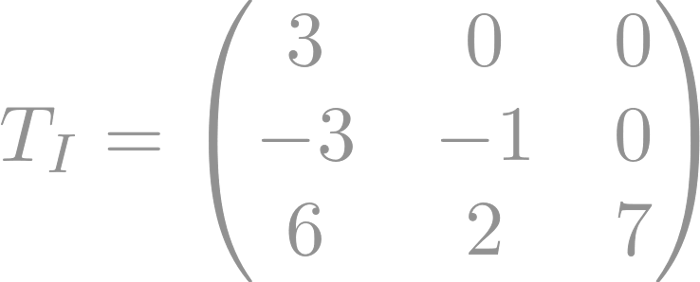
Este tipo de matriz, ya sea triangular superior o inferior, es conveniente para resolver sistemas de ecuaciones lineales mediante el método de eliminación gaussiana y también se utiliza en algoritmos de optimización y en la diagonalización.

Matriz simétrica y antisimétrica

Una matriz se considera simétrica si se trata de una matriz cuadrada que es igual a su transpuesta. Es decir, si una matriz A es simétrica, entonces A^T (transpuesta de A) es igual a A.

Este sería un ejemplo de matriz simétrica:

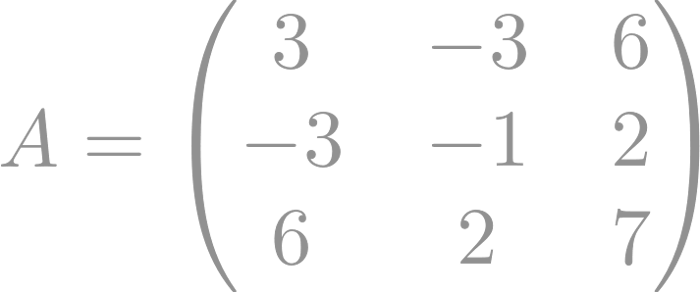
La matriz simétrica tiene propiedades interesantes y se utiliza en diversos campos, como la mecánica, física y estadística.

Por otro lado tenemos la matriz antisimétrica, que se trata de una matriz cuadrada que cumple la propiedad de que la matriz transpuesta (A^T) es igual a la matriz opuesta (-A).

Aquí tenemos un ejemplo de matriz antisimétrica:

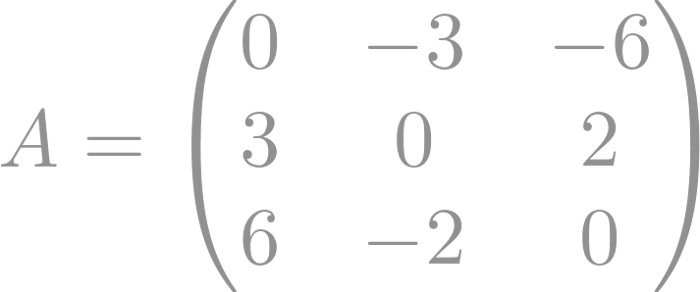
La matriz antisimétrica también tiene propiedades interesantes y es útil en el estudio de rotaciones y propiedades físicas como el momento angular.

Aplicaciones del álgebra matricial

El álgebra lineal es ampliamente utilizado en la resolución de sistemas de ecuaciones lineales. Los sistemas de ecuaciones pueden representar situaciones en las que varias incógnitas están relacionadas mediante ecuaciones lineales. La representación matricial de estos sistemas permite resolverlos de manera eficiente utilizando técnicas como la eliminación gaussiana o la descomposición LU.

Las transformaciones lineales son funciones que mantienen la estructura lineal de un espacio vectorial. Estas transformaciones se pueden representar mediante matrices, lo que facilita la comprensión y manipulación de estas operaciones. Por ejemplo, transformaciones de rotación, reflexión y escalado en dos dimensiones se pueden representar con una matriz.

El álgebra lineal es esencial en el análisis de redes y sistemas complejos. Las redes pueden representar sistemas sociales, comunicación, transporte, entre otros. Mediante la representación matricial, se pueden analizar propiedades y comportamientos de estas redes, como la centralidad de los nodos, detección de comunidades y la propagación de información.

En programación e informática, la matriz es ampliamente utilizada para almacenar y procesar datos en forma tabular. Por ejemplo, en el desarrollo de aplicaciones de hojas de cálculo, procesamiento de imágenes, bases de datos y gráficos, una matriz nos permite organizar y manipular grandes conjuntos de datos de manera eficiente.

El procesamiento de imágenes y gráficos también se beneficia del álgebra lineal en diversas técnicas. Operaciones como la convolución, transformaciones de perspectiva, filtrado y reducción de ruido se pueden realizar eficientemente mediante matrices y operaciones matriciales.

Finalmente, el álgebra lineal es esencial en el campo del aprendizaje automático (machine learning) y el análisis numérico. Muchos algoritmos de aprendizaje automático, como regresión lineal, clasificación, y descomposición en valores singulares (SVD), se basan en conceptos matriciales. Además, en el análisis numérico, la resolución de ecuaciones diferenciales, la optimización y métodos iterativos utilizan matrices y operaciones matriciales para obtener soluciones aproximadas a problemas complejos.

Aprende Matemáticas desde Cero - Álgebra Matricial

Como hemos visto, la matriz es una herramienta matemática esencial que ha demostrado su utilidad en una amplia variedad de aplicaciones y disciplinas. Desde el análisis de datos hasta la ingeniería y la ciencia, las matrices nos brindan una forma eficiente y poderosa de representar y manipular información. Esperamos que este post de blog haya sido útil para comprender la importancia de las matrices y cómo se aplican en el mundo real. Te invitamos a explorar más a fondo este fascinante tema y descubrir cómo las matrices pueden mejorar tu comprensión y solución de problemas en tu campo de interés. ¡Aprovecha el poder de las matrices y desata tu potencial analítico!