Como solemos comentar en nuestros cursos de Inteligencia Artificial, en los modelos de machine learning el objetivo es encontrar los parámetros del modelo que minimizan una función de costes. La cual se encarga de medir nuestro error en la predicción o en la clasificación de las observaciones. Hoy vamos a ver el problema del desvanecimiento del gradiente en IA.
En redes neuronales se usa el algoritmo de gradiente descendente. Que va realizando iteraciones sobre los parámetros proporcionales al valor negativo del gradiente en el punto actual. El algoritmo usa la propagación hacia atrás para poder calcular el valor del gradiente y corregir adecuadamente los parámetros del modelo. Para que así el error de predicción sea cada vez menor.
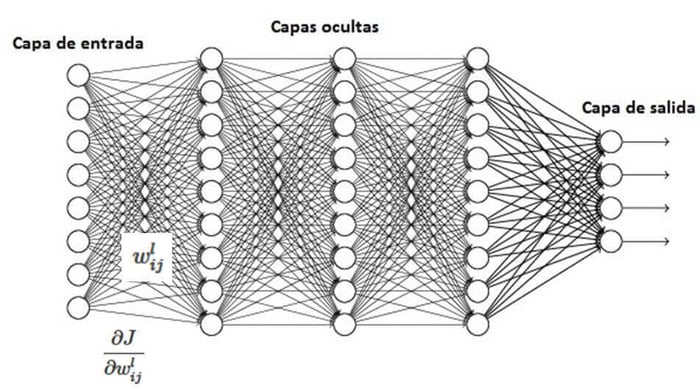
Así pues, para los parámetros de la capa l se repetiría el siguiente proceso de corrección iterativo hasta que los parámetros converjan (o hasta un número máximo de iteraciones prefijado):
$latex w_{ij}^l \leftarrow w_{ij}^l - \alpha \frac{\partial J}{\partial w_{ij}}&s=3$
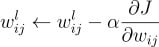
¿Qué ocurre cuando la red tiene muchas capas?
En la siguiente red neuronal simple con $latex n$ capas ocultas y con una neurona por capa, la salida de cada neurona se calcula multiplicando la salida de la neurona previa por el parámetro $latex W_n$ y aplicando la función de activación $latex f(z)$. La función de costes $latex J$ al final de la red neuronal nos devuelve el error de la misma. Y es la que se utiliza para modificar el resto de parámetros de la red neuronal a través del método del gradiente descendente.
Para obtener cuanto afecta el peso $latex w_1$ al error global, hay que calcular la derivada de $latex J$ con respecto al parámetro de la primera capa. Utilizando la regla de la cadena daría como resultado:
$latex \frac{\partial J}{\partial w_1} = \frac{\partial J}{\partial salida}\cdot \frac{\partial salida}{\partial capa_n} \cdots \frac{\partial capa_2}{\partial capa_1}\cdot\frac{\partial capa_1}{\partial w_1}&s=3$
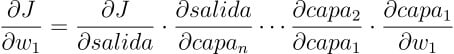
Podemos calcular también el valor de un ejemplo de las derivadas entre capas:
$latex \frac{\partial capa_{k+1}}{\partial capa_k} = \frac{\partial f(z_k)}{\partial z_k}w_{k+1}&s=3$
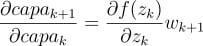
donde la variable $latex z_k=capa_k\cdot w_{k+1}$.
Si la función de activación elegida $latex f(z)$ es la función sigmoide, una de las más comunes, debido a que su derivada siempre está acotada entre 0 y 0.25, cuando tenemos una red con muchas capas el valor de gradiente cada vez es más cercano a 0 ya que estamos multiplicando muchas veces valores que son más pequeños que 1. Debido a este problema, las primeras capas de una red neuronal son las más lentas y difíciles de entrenar. Ya que el valor del gradiente que se usa para actualizarlas en cada iteración del entrenamiento es muy pequeño. Y esto causa otro problema adicional: que si las primeras capas no están bien entrenadas, el problema se arrastra a las capas posteriores.
Problema parecido en las redes neuronales
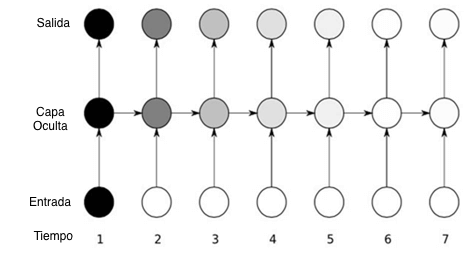
El problema es similar en las redes neuronales recurrentes (RNR). Las RNR modelan datos en los que es importante la estructura temporal, como frases con palabras, series temporales y también se entrenan usando la propagación hacia atrás. Cada intervalo de tiempo se modela como una capa y por lo tanto una RNR sería equivalente a una red con tantas capas como intervalos de tiempo y sufrirían el mismo problema de desvanecimiento del gradiente.
En la imagen podemos ver cómo la sensibilidad a los valores de la entrada en una RNR decae con el tiempo. De esta forma es muy difícil que la red recuerde dependencias temporales largas.
¿Qué soluciones hay al problema del desvanecimiento del gradiente?
Como hemos dicho antes, la derivada de la función sigmoide es menor o igual que 0.25, pero si cogemos como función de activación la función Rectificadora Lineal Unitaria (ReLU), cuya derivada es siempre igual a 1 por encima de 0, podríamos obtener mejores soluciones.
Para el caso de las RNR, la solución pasa por usar las llamadas LSTMs (Long Short-Term Memory Networks). Donde cada nodo o neurona es una célula de memoria. De esta forma la red es capaz de retener información de entradas anteriores en el tiempo y tener en cuenta dependencias temporales largas.
Si quieres verlas más en detalle, investigar su implementación y el detalle matemático de las mismas, te recomendamos echarle un vistazo a nuestro curso Deep Learning de la A a la Z que tienes disponible en Udemy.
Por último, queremos invitarte a nuestra Ruta de Aprendizaje para ser un experto en Inteligencia Artificial.
