El mundo de las Series Temporales es todo un campo de suma importancia dentro del análisis de datos y la ciencia de datos puesto que constantemente tenemos observaciones que dependen del día de la semana, del mes o del año.
Por tanto, la idea de nuestro artículo de hoy es meternos de lleno en una introducción inicial hacia el mundo de las Series Temporales y su correcto tratamiento desde el punto de vista analítico y estadístico.
Primeras Nociones de Series Temporales
Vamos a empezar con la definición de serie temporal. Una serie temporal o serie de tiempo es una secuencia de información que pone en correspondencia un período de tiempo a cada valor.
El valor puede ser prácticamente cualquier cosa medible que dependa del tiempo de alguna manera. Como por ejemplo precios, humedad o número de personas.
No existen limitaciones con respecto al tiempo total de nuestras series de tiempo. Todo lo que necesitamos es un punto de partida y un punto final. Entre esos dos puntos, habrá muchos otros puntos. Tantos como queramos.
El intervalo de tiempo entre un punto en el tiempo y el siguiente, se llama período de tiempo.
Con qué periodicidad los valores del conjunto de datos se registran se conoce como la frecuencia del conjunto de datos.
Para poder analizar series temporales de una manera significativa, todos los períodos de tiempo deben ser iguales y claramente definidos, lo que daría como resultado una frecuencia constante. Esta frecuencia es una medida del tiempo y puede variar desde unos pocos milisegundos hasta varias décadas. Sin embargo, veremos los más usuales son cada minuto, cada hora, cada día, cada semana, cada mes, cada cuatrimestre, cada año, etc.
Además, se espera que los patrones que se observen en las series de tiempo persistan o continúen existiendo en el futuro.
Un ejemplo muy usual son los datos meteorológicos que suelen hacer frente a la tarea de pronosticar el clima durante varios días hacia el futuro. Para hacer predicciones precisas de manera consistente, hay que analizar datos pasados. Pero claro, si los datos no se ordenan cronológicamente, encontrar el patrón correcto sería extremadamente difícil. Por ejemplo, simplemente conocer la temperatura más alta de los últimos cinco días sería inútil, a menos que sepamos qué valor de temperatura corresponde a cada día.
En el mundo de los negocios, los datos de series de tiempo se aplican muchísimo en análisis de finanzas para los inversores y los propietarios de las empresas. Es crucial determinar si los precios arrojan ganancias y las ventas aumentarán o disminuirán en el futuro. Por lo tanto, un tema común en el análisis de series de tiempo es determinar la estabilidad o la volatilidad de los mercados financieros.
Estacionariedad de las Series Temporales
Series Estacionarias
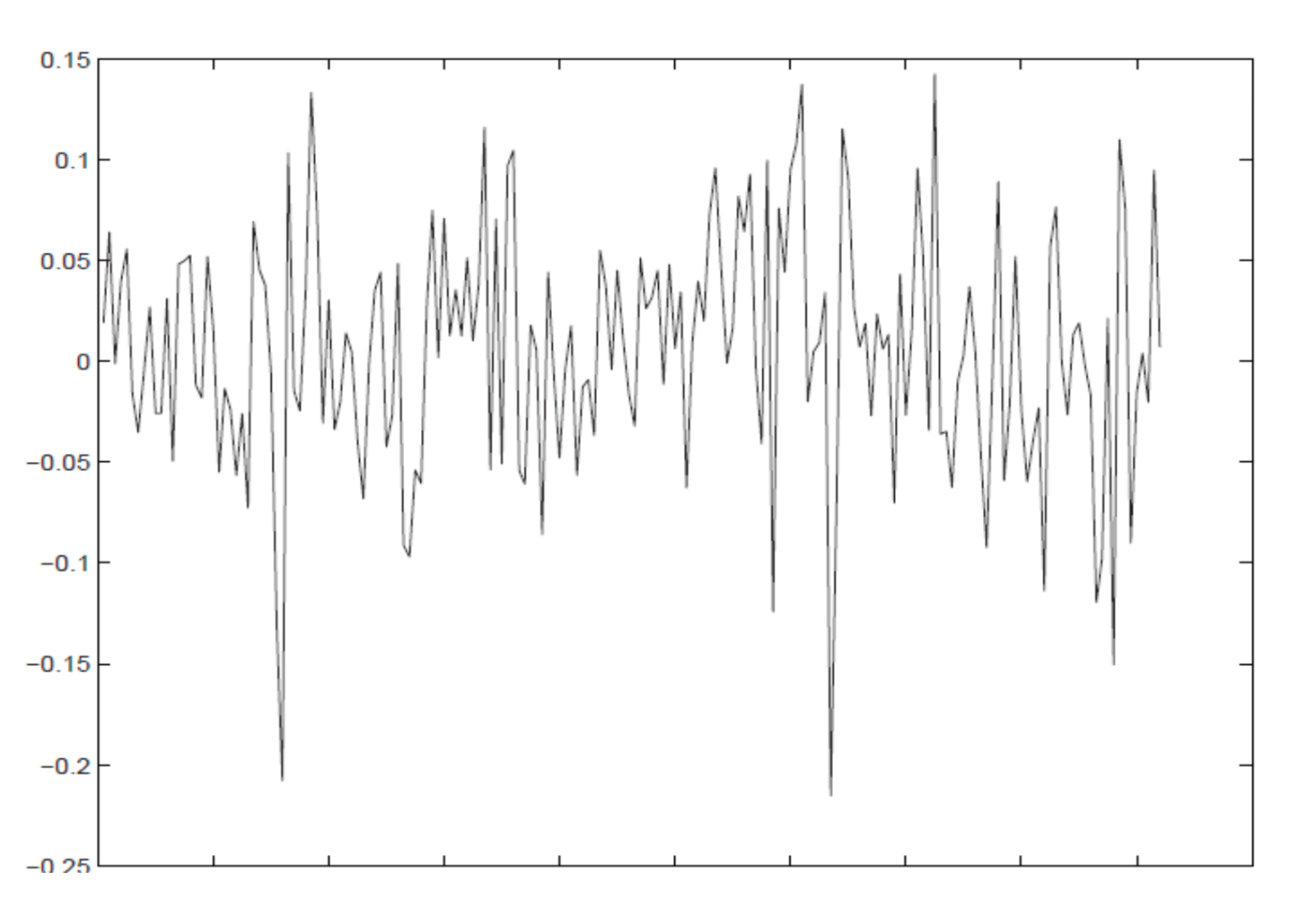
La figura es un ejemplo de una serie estacionaria. Da el rendimiento mensual promedio de la Bolsa de Madrid durante el período de 1988 a 2000 medido por el Índice General. Observa que los valores de la serie parecen moverse alrededor de un rendimiento mensual fijo. No hay tendencias crecientes o decrecientes con el tiempo.
Series No Estacionarias
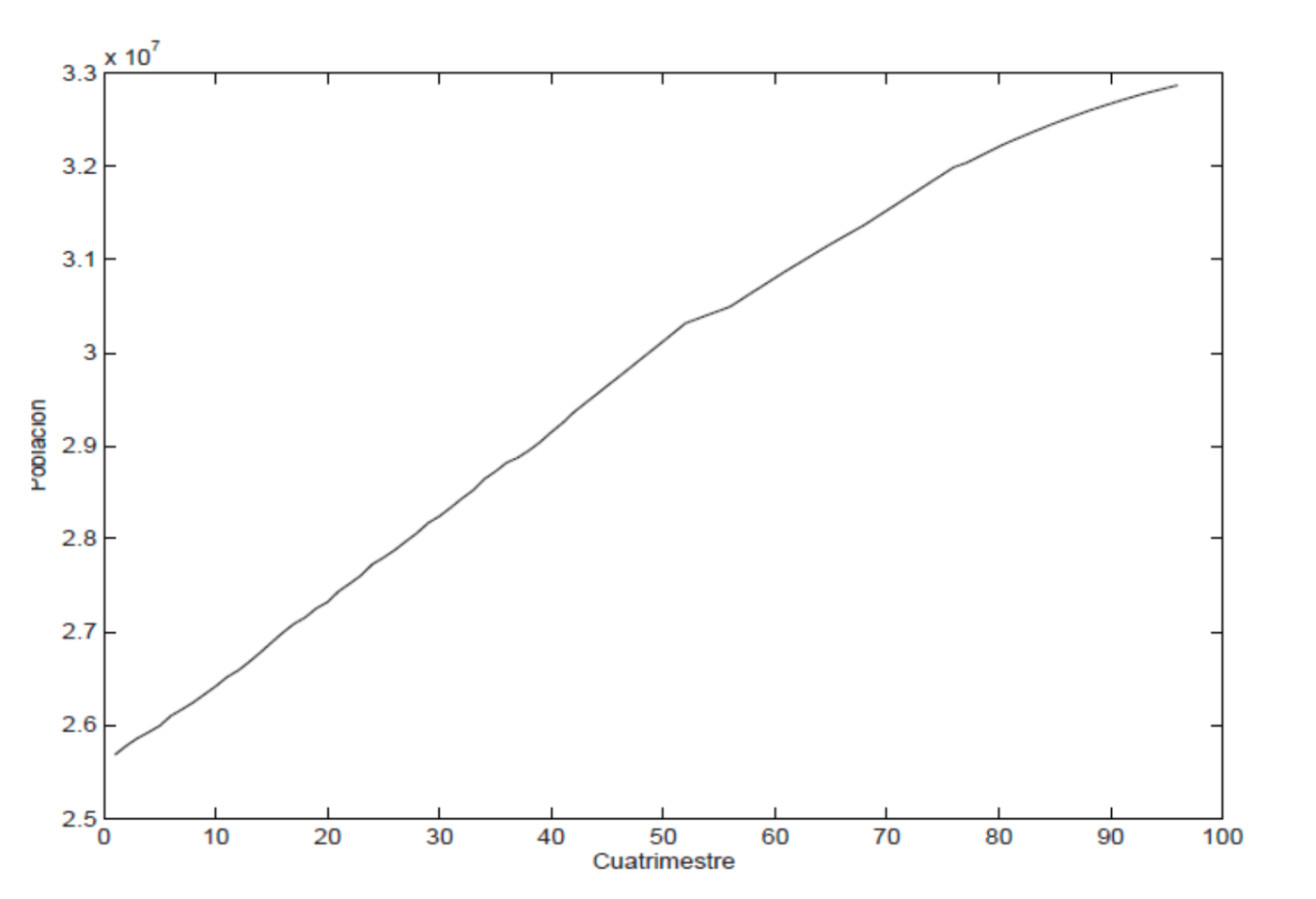
Sin embargo, este otro ejemplo muestra una serie que, a diferencia de la anterior, no es claramente estable en el tiempo, y es lo que llamamos no estacionario.
La serie corresponde a la población española mayor de 16 años al final de cada trimestre durante el período de 1977 a 2000. Observa en el gráfico que la serie no es estable, ya que su nivel aumenta con el tiempo. Decimos que la serie tiene una tendencia clara y positiva.
La mayoría de las series económicas y sociales no son estacionarias (estables) y muestran tendencias. En este caso, la tendencia es aproximadamente lineal, aunque la pendiente de la línea que encajamos en la primera mitad de la muestra sería algo mayor que la que obtendríamos en la segunda. Esto sugiere que quizás el crecimiento anual de la población está cambiando con el tiempo.
La tendencia de la serie sería entonces variable en el tiempo en lugar de constante. Esta propiedad es típica en series reales en la práctica, donde es poco probable que observemos una tendencia constante durante largos períodos de observación.
La no estacionariedad puede ser de diferentes formas:
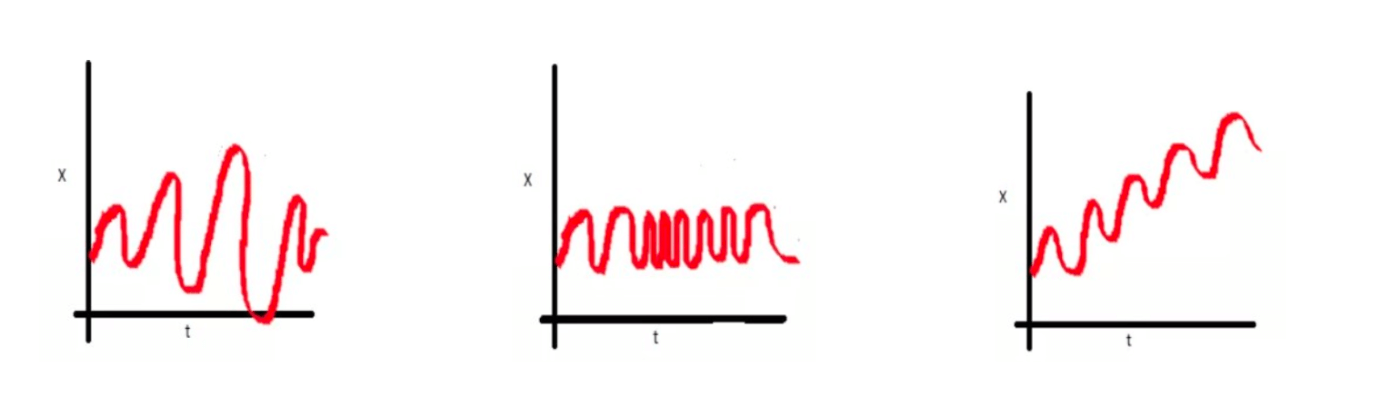
Una serie es estacionaria cuando es estable a lo largo del tiempo, es decir, cuando la media y la varianza son constantes en el tiempo y, además, no presenta tendencia. Esto se refleja gráficamente en que los valores de la serie tienden a oscilar alrededor de una media constante y la variabilidad con respecto a esa media también permanece constante en el tiempo.
La series NO estacionarias son series en las cuales la tendencia y/o variabilidad cambian en el tiempo. Los cambios en la media determinan una tendencia a crecer o decrecer a largo plazo, por lo que no oscilaría alrededor de un valor constante.
Prueba Dickey-Fuller de Estacionariedad
Para llevar a cabo un análisis adecuado de series de tiempo es vital determinar si los datos siguen un proceso estacionario o no estacionario. Por suerte para nosotros, en el siglo XX, los estadísticos David Dickey y Wayne Fuller desarrollaron una prueba para ayudarnos. El método para verificar si un conjunto de datos proviene de un proceso estacionario, se conoce como la prueba Dickey-Fuller o prueba de DF en abreviatura.
La prueba está basada en un contraste de hipótesis. Vamos a tener como hipótesis nula que la serie es No Estacionaria. Con lo cual la alternativa es que sí lo es.
Cuando hacemos el contraste de hipótesis, siempre tenemos que calcular el valor de un estadístico de prueba, que dependerá de los valores de la muestra y de nuestra hipótesis nula.
El valor del estadístico se compara con un valor crítico en la tabla Dickey Fuller. Si el estadístico de prueba o de contraste es inferior al valor crítico rechazamos la hipótesis nula. Lo que significa que entonces los datos provienen de un proceso estacionario.
Otra manera de llegar a estas conclusiones es a través del p-valor. El p-valor se puede interpretar como el valor que representa cuán probable es la hipótesis nula. Si es un valor muy cercano a cero significa que esa hipótesis es poco probable y habría que rechazarla.
¿Cómo sabemos si es un valor muy bajo, pero suficiente para rechazar la Hipótesis nula?
Porque siempre que hagamos algo en inferencia vamos a tener un nivel de confianza, por ejemplo, el 95%, y lo que le falta a eso para llegar al 100% es nuestro nivel de significación, es decir 5%=0.05. Entonces compararíamos el p-valor con el nivel de significación. Si es más pequeño diremos que es suficientemente bajo para rechazar la Hipótesis nula.
En Python lo haremos con el método sts.adfuller del paquete stattools.
En R lo haremos con la función adf.test del paquete tseries.
Estacionalidad de las Series Temporales
La estacionalidad sugiere que ciertas tendencias aparecerán de forma cíclica. Por ejemplo, las temperaturas suben y bajan según las horas del día y los meses del año. Estos son dos ejemplos distintos de patrones estacionales que observamos en nuestra vida, el cambio durante el día y el cambio durante un año completo.
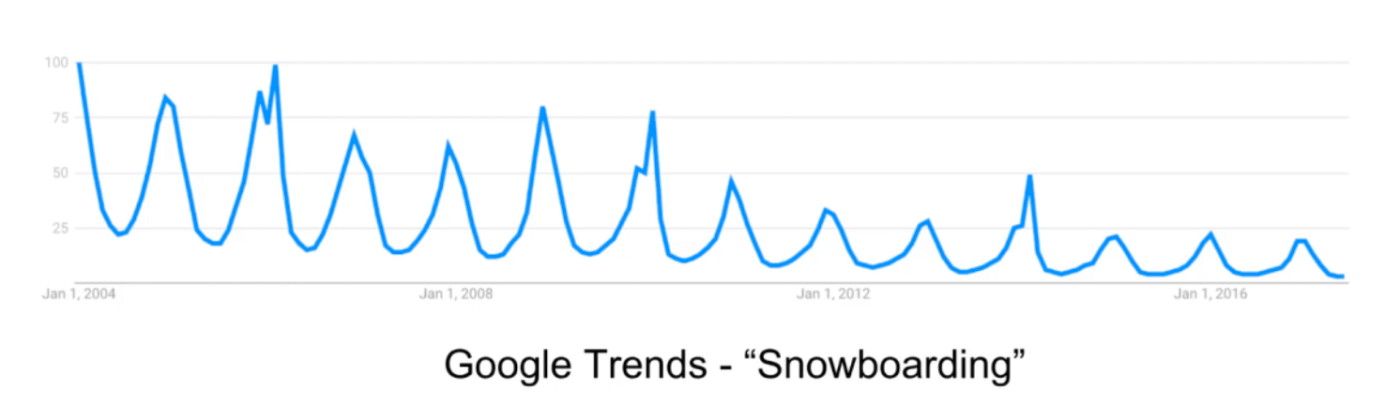
Hay varias formas de comprobar si existe estacionalidad.
Un enfoque es descomponer la secuencia de la serie temporal en tres efectos.
- Tendencia
- Estacional
- Residual
Por supuesto, la tendencia representa el patrón consistente en todos los datos. El efecto estacional expresa todos los efectos cíclicos debido a la estacionalidad. Finalmente, los residuos son el error de predicción, o la diferencia entre los datos reales y el modelo que ajustamos.
El tipo más simple de descomposición es la descomposición clásica. Con ella esperamos una relación lineal entre las tres partes y la serie de tiempo observada. Hay dos enfoques principales en la descomposición clásica:
- Aditivo
- Multiplicativo
El aditivo supone que, para cualquier período de tiempo, el valor observado es la suma de la tendencia, más el efecto estacional, más el residual, para ese período. Del mismo modo, la descomposición multiplicativa supone que la serie original es un producto de los tres efectos.
El Python, el paquete de modelos de estadística incluye un método llamado seasonal_decompose que significa descomposición estacional, que coge una serie de tiempo y la divide en esos tres efectos.
En R usaremos la función decompose del paquete stats.
Autocorrelación
Como su nombre lo indica, la autocorrelación representa la correlación entre una secuencia y sí misma. Más precisamente, dentro de las Series Temporales mide el nivel de semejanza entre una secuencia de hace varios períodos y los datos reales.
La secuencia de hace varios períodos atrás se llama “retraso” o “lag” en inglés, porque es una versión retrasada de la original. Por ejemplo, si calculamos la autocorrelación para una serie de tiempo con frecuencia diaria, estamos determinando cuántos de los valores de ayer se parecen a los valores de hoy. Si la frecuencia es, en cambio, anual, entonces la autocorrelación medirá las similitudes de año en año.
Ruido Blanco
El ruido blanco en las Series Temporales es un tipo especial de serie temporal donde los datos no siguen un patrón. Como en el ruido blanco no encontramos ningún patrón, no se puede predecir en el futuro. Es decir, el ruido blanco no es predecible.
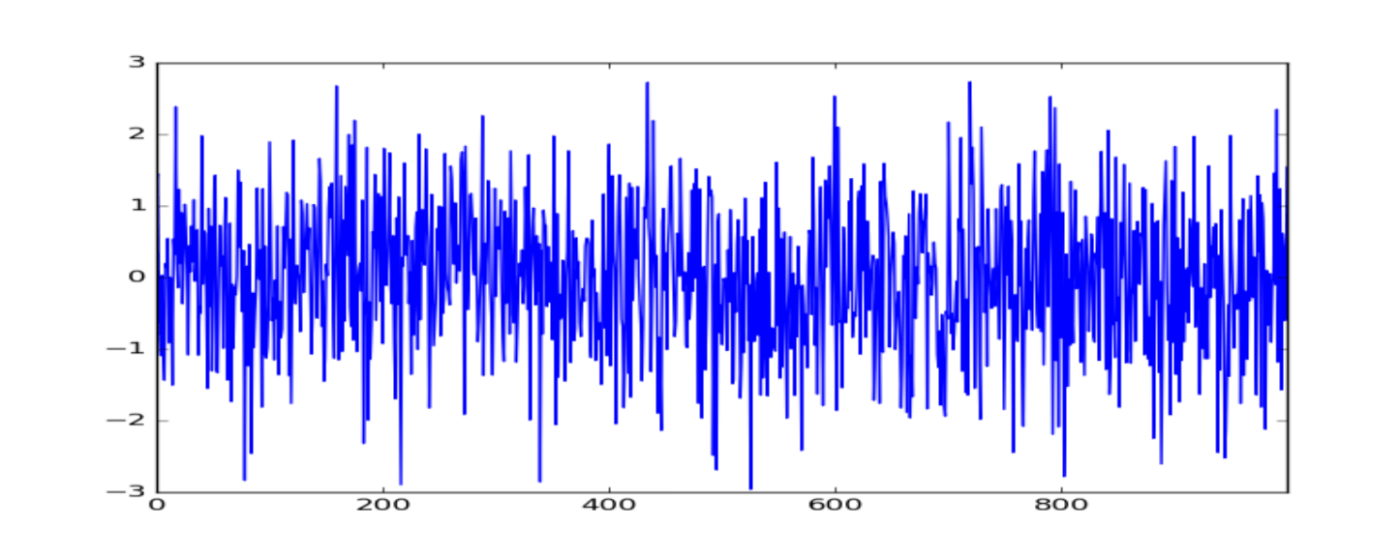
Además, para que una serie se pueda considerar como ruido blanco, necesita satisfacer las siguientes tres condiciones:
- Media constante
- Varianza constante
- No tener autocorrelaciones significativas en ningún período.
ACF
En series temporales es vital poder calcular y comparar los valores de autocorrelación entre diferentes retrasos. Para ello, necesitamos introducir la función de autocorrelación o ACF (autocorrelation function).
La función de autocorrelación proporciona la autocorrelación para cualquier retraso que consideremos. La alternativa sería encontrar manualmente la correlación entre nuestros datos originales y múltiples retrasos de sí misma.
En Python usaremos la función plot_acf y en R la función acf.
Un ejemplo sería:
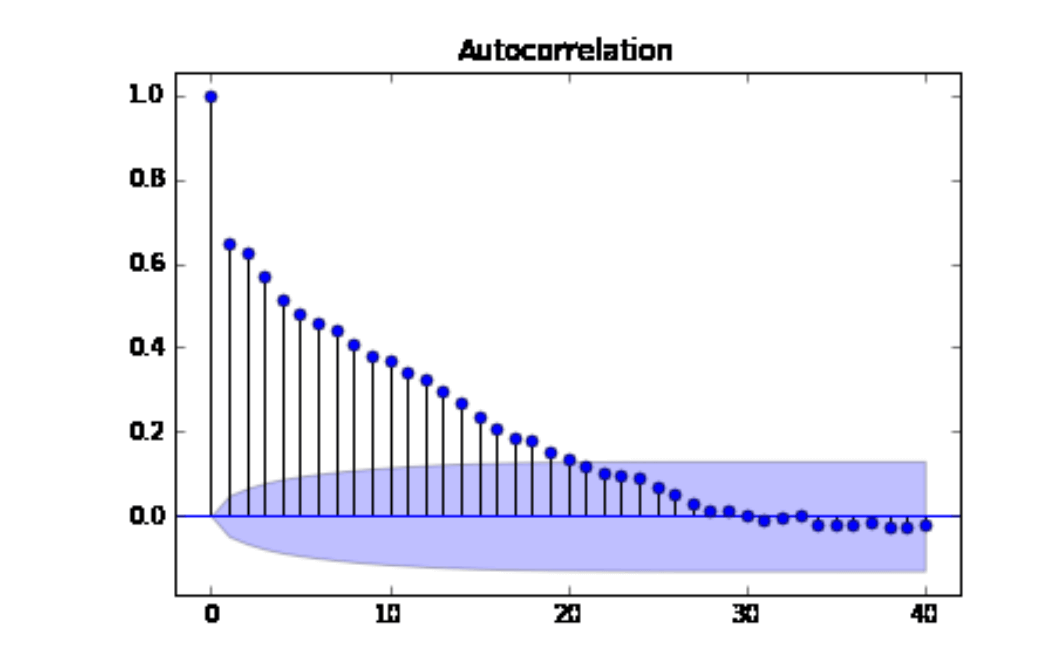
En el gráfico de Series Temporales anterior, los valores en el eje x representan los retrasos, que en este caso van hasta 40, ya que eso es lo que se estableció.
Los números a la izquierda en el eje vertical representan los posibles valores para el coeficiente de autocorrelación. La correlación solo puede tomar valores entre -1 y 1.
Las líneas en el gráfico representan la autocorrelación entre la serie de tiempo y una versión retrasada de sí misma. La primera línea indica la autocorrelación con retraso de 1 período de tiempo, la segunda línea representa la autocorrelación para hace dos períodos y así sucesivamente.
La primera línea es uno porque la correlación entre un valor y sí mismo siempre será uno.
El área azul alrededor del eje x representa la significación de los valores de autocorrelación. Es decir, mide si son significativamente distintos de cero, lo que sugiere la existencia de autocorrelación para ese retraso específico.
Si los coeficientes son significativos, es un indicador de la dependencia del tiempo en los datos.
La función ACF se utilizará para investigar cuántos retrasos son necesarios en el modelo de medias móviles. Y para investigar si los residuos son ruido blanco, es decir, si las correlaciones son no significativas para los residuos.
PACF
La autocorrelación mide la similitud entre una serie temporal y unas versiones anteriores de sí misma. Sin embargo, los coeficientes también capturan efectos de los momentos anteriores de manera indirecta. Por indirecta nos referimos a todos los demás canales a través de los cuales los datos del pasado afectan a los datos actuales. Si deseamos determinar solo la relación directa entre la serie de tiempo y su versión retrasada, necesitamos calcular la autocorrelación parcial.
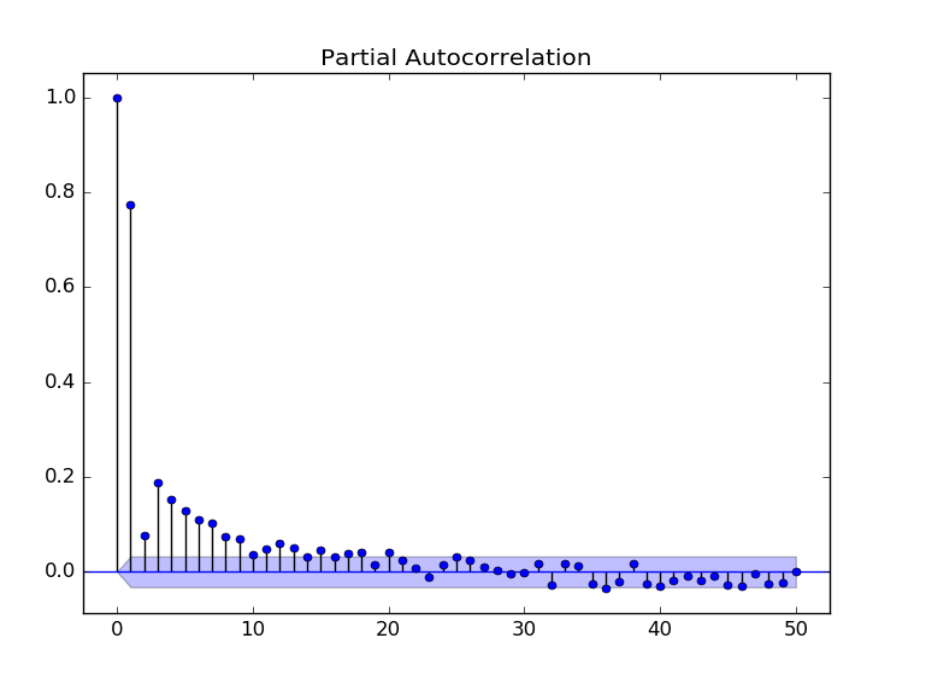
La función PACF se utilizará para investigar cuántos retrasos es necesario en el modelo autorregresivo.
En Python usaremos la función plot_pacf y en R la función pacf.
Conclusión
Si quieres aprender más acerca de las Series Temporales y los modelos para su análisis, te invitamos a nuestra Ruta de Análisis de Datos con R y con Python disponible en Frogames Formación donde durante más de 500 horas de vídeos y centenares de ejemplos verás cómo poder analizar todo tipo de datos en ambos lenguajes, y elaborar modelos de predicción de ventas futuras usando Series Temporales.
¡Nos vemos en clase!