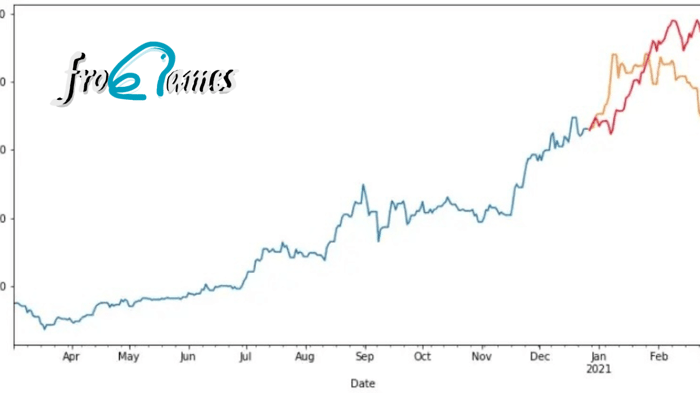
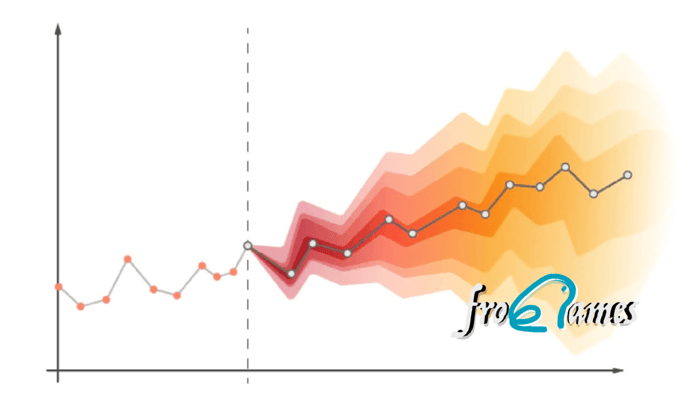
Después de un análisis descriptivo y exploratorio de las series de tiempo, y de ver los modelos básicos para predecir los siguientes datos de una serie temporal, no nos queda más que ver los modelos más avanzados para predecir el futuro en base a un modelo de series temporales.

El procedimiento general es el que ya vimos en la primera parte y que aquí recordamos una vez más:

1. Escoger el modelo
2. Dividir los datos en datos de entrenamiento y datos de prueba
3. Ajustar el modelo a los datos de entrenamiento
4. Evaluar el modelo en los datos de prueba
5. Re-ajustar el modelo con todos los datos
6. Predecir los datos futuros en Series de Tiempo

Modelos Max

Los modelos MAX son modelos que consideran información exógena para explicar la variable endógena (la serie que estemos estudiando). Vamos a tener versiones MAX de todos los modelos estudiados: ARMAX, ARIMAX, SARMAX y SARIMAX.

Ejemplo, modelo ARMAX de orden simple, donde 𝑌 es la variable exógena:

𝑥𝑡 = 𝑐 + 𝛽𝑌 + 𝜑1𝑥𝑡−1 + 𝜃1𝜖𝑡−1 + 𝜖𝑡

La variable exógena puede ser una serie o varias series (varias variables).

Por lo general mejoran mucho al modelo, pero tienen la desventaja de que para predecir datos de futuro, como en el futuro no conocemos los valores de esas variables exógenas, no podríamos usar esto, a no ser que estimemos de alguna forma los valores de esas variables extra. Esto tiene que ver con otros modelos que se llaman VAR.

Modelos Var

Es un modelo multivariante al que le pasamos varias variables para estimar cada serie en dependencia de las demás. Por ejemplo para estimar los precios de mercado, cada uno, en dependencia del otro conjunto de precios.

Modelos Arch y Garch

Son modelos para estimar la volatilidad (variabilidad y cambios) en una serie temporal. Cuando los inversores están interesados en hacer grandes compras a largo plazo, a menudo buscan estabilidad.

Es por eso por lo que surge la necesidad de modelos especiales que midan la volatilidad. Para empezar, cuando hablamos de volatilidad, estamos hablando de la magnitud de los residuos. No nos importa si son positivos o negativo. Solo nos importa cuán volátiles sean nuestras predicciones.

Dado que buscamos estabilidad, eso explica por qué la volatilidad es sinónimo de variación y por qué queremos para evitarlo una varianza más baja, lo que indicaría mayor estabilidad que a su vez sugiere un riesgo menor. Por lo tanto, medir la volatilidad es clave cuando queremos seguridad en nuestras inversiones.

Una solución es propuesta por los modelos autorregresivos con heterocedasticidad condicional, que en inglés se diría Autoregressive Conditional Heteroscedasticity Model, o modelo ARCH.

Lo primero, es que, a diferencia de la familia ARIMA, los ARCH consisten en varias ecuaciones, una para la media y otra para la varianza.

La ecuación para la varianza de un ARCH(q), que mide la varianza condicional en función de residuos pasados, es:

𝜎𝑡^2 = 𝛼0 + 𝛼1𝜖𝑡−1 ^2 + 𝛼2𝜖𝑡−2 ^2 + ⋯ + 𝛼𝑞 𝜖𝑡−𝑞 ^2

Y la ecuación para la media junto con la que estima el valor actual de la serie es:

𝑥𝑡 = 𝑐0 + 𝜑1𝜇𝑡−1 + 𝜖𝑡

Para este método se investiga la PACF.

Una posible mejora de los modelos ARCH es incluir también valores pasados, además de los residuos al cuadrado. Pero ¿cuáles serían exactamente estos valores pasados?

Pensemos. Incluir valores pasados de los retornos en este caso no tendría mucho sentido, ya que generalmente contamos con ellos en la ecuación media. Si queremos trazar una idea paralela a lo que hacíamos con el modelo ARMA, debemos incluir algunos componentes autorregresivos, y como estamos trabajando con varianzas, vamos a incluir esas variaciones condicionales pasadas para ayudarnos a explicar las variaciones condicionales actuales.

Ya que los períodos de alta volatilidad son seguidos por períodos de alta volatilidad y los períodos de baja volatilidad son seguidos por tales con baja volatilidad, eso significa que agregar variaciones condicionales pasadas debería servir como un gran punto de referencia para las estimaciones del presente.

Una varianza condicional pasada ya incluiría en sí misma los efectos de los residuos al cuadrado anteriores. Esto haría que agregar más residuos al cuadrado anteriores sea redundante.

Es por eso por lo que el siguiente modelo se llama Generalized Autorregresive Conditional Heteroscedasticity Model o simplemente GARCH. El modelo GARCH es una extensión del modelo ARCH, donde agregamos varianzas condicionales pasadas a la ecuación de varianza.

La intuición detrás de esto proviene de que la volatilidad pasada nos da información sobre patrones consecutivos. Por lo tanto, si incluimos la varianza condicional del último período tendremos una especie de punto de referencia sobre qué debemos esperar.

Un GARCH(1,1) tendría como ecuación de la varianza:

𝜎𝑡^2 = 𝛼0 + 𝛼1𝜖𝑡−1 ^2 + 𝛽1𝜎𝑡−1 ^2

Donde 𝛽1 es el coeficiente del nuevo término que hemos incluido explicando la varianza condicional del período anterior.

Cuando se trata de la variación de precios del mercado, ningún modelo GARCH de orden superior supera al modelo GARCH(1,1) simple.

Modelos Auto Arima para Series de Tiempo

Es el método automático para estimar el mejor modelo que se ajusta a la serie temporal. Por defecto tiene parámetros fijados, como por ejemplo el orden máximo que puede tomar el modelo. En la práctica, se recomienda hacer un análisis exploratorio antes para ver si hay un orden máximo superior que deberíamos considerar, superior al que viene por defecto en la función.

Pros:

1. Ahorra tiempo
2. Elimina ambigüedades
3. Reduce el riesgo de error humano

Contras:

1. Poner ciegamente la fe en un solo modelo
2. No se ve realmente si los demás modelos funcionan mejor o no
3. Requiere cierta experiencia en el tema
4. Error humano

En Python: auto_arima del paquete pmdarima.

En R: auto.arima del paquete forecast.

Y para ir directos al código para analizar series de tiempo

Librerías de Python que recomendamos consultar para analizar Series de tiempo:

1. ARMA
2. ARIMA
3. SARIMAX
4. ARCH
5. Auto arima
6. Prophet de Facebook.
7. Yfinance

Librerías de R que recomendamos consultar para analizar correctamente las Series de Tiempo:

1. Paquete lubridate, que no es específico de series temporales sino más bien de pre-procesado de datos. Lo usaremos para formatear la fecha y el tiempo.
2. Paquete tseries, que también nos permitirá trabajar con series temporales, modelar y graficar. También lo usaremos para testear por estacionariedad.
3. Paquete forecast que tiene muchas funciones, como la función AutoArima que es un método de modelado automático. También hay un montón de herramientas para limpiar el dataset de datos faltantes, de atípicos o outliers, tiene muchas herramientas gráficas para modelar series de tiempo y permite modelar los pronósticos hacia el futuro.

Conclusión

Si quieres aprender más acerca de las Series Temporales y los modelos para su análisis, te invitamos a nuestra Ruta de Análisis de Datos con R y con Python disponible en Frogames Formación donde durante más de 500 horas de vídeo y centenares de ejemplos verás cómo poder analizar todo tipo de datos en ambos lenguajes, y elaborar modelos de predicción de ventas futuras usando Series Temporales.