En este artículo, repasaremos todo el proceso de creación de un modelo de aprendizaje automático utilizando el famoso conjunto de datos del Titanic, utilizado por personas de todo el mundo. Este conjunto de datos proporciona información sobre el destino de los pasajeros del Titanic, resumida según su estatus económico (clase), sexo, edad y supervivencia.
Inicialmente aprendí acerca de este problema en una competición de kaggle.com, titulada “Titanic: Machine Learning from Disaster”. En este desafío, se nos pedía predecir si un pasajero del Titanic habría sobrevivido o no. Aquí os voy a detallar un análisis completo de cómo lo hice.
RMS Titanic ⚓
El RMS Titanic fue un transatlántico británico que se hundió en el océano Atlántico norte en las primeras horas de la mañana del 15 de abril de 1912, después de chocar con un iceberg durante su viaje inaugural de Southampton a Nueva York. Se estima que había 2,224 pasajeros y tripulantes a bordo del Titanic, y más de 1,500 murieron, lo que lo convierte en uno de los desastres marítimos comerciales más mortales de la historia moderna.
El Titanic fue el barco más grande en servicio en el momento en que entró en funcionamiento y fue el segundo de tres transatlánticos de la clase olímpica operados por la White Star Line. Fue construido en el astillero Harland and Wolff en Belfast. Thomas Andrews, su arquitecto, murió en el desastre.
Importación de las librerías 📚
Obtención de los Datos 📊
Exploración y Análisis de los Datos 🔍
El conjunto de entrenamiento tiene 891 ejemplos y 11 características más la variable objetivo (survived). 2 de las características son flotantes, 5 son enteros y 5 son objetos. A continuación, se describen brevemente las características:
survival: Supervivencia
PassengerId: ID único de un pasajero.
pclass: Clase del billete
sex: Sexo
Age: Edad en años
sibsp: Número de hermanos/esposos a bordo
parch: Número de padres/hijos a bordo
ticket: Número de billete
fare: Tarifa del pasajero
cabin: Número de la cabina
embarked: Puerto de embarque
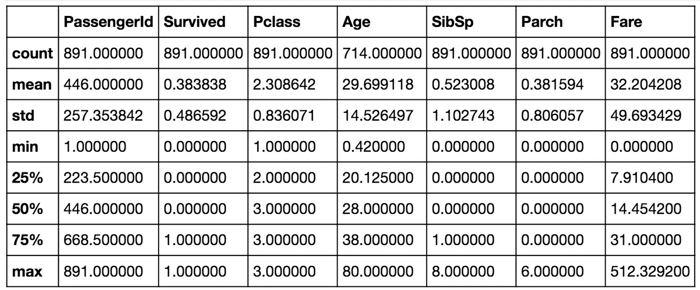
En la tabla anterior, podemos ver que el 38% del conjunto de entrenamiento, los pasajeros del Titanic sobrevivieron a la tragedia. También observamos que las edades de los pasajeros oscilan entre 0.4 y 80 años. Además, ya podemos detectar algunas características que contienen valores faltantes, como la característica 'Age'.
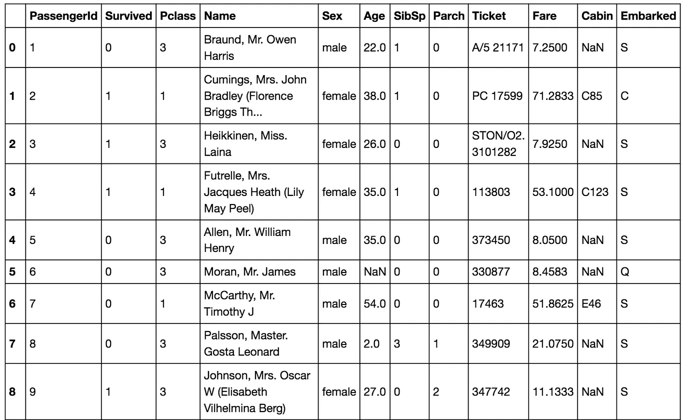
En la tabla anterior, podemos observar que necesitamos convertir muchas características en variables numéricas para que los algoritmos de aprendizaje automático puedan procesarlas. También notamos que las características tienen rangos muy diferentes, lo que requerirá que las pongamos en una escala más uniforme. También se pueden detectar más características con valores faltantes (NaN = not a number), que necesitamos abordar.
Análisis de los Datos Faltantes ❌
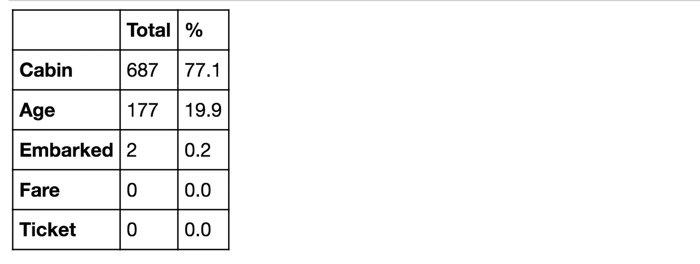
La característica Embarked tiene solo 2 valores faltantes, lo cual es fácil de llenar. Será mucho más complicado tratar con la característica 'Age', que tiene 177 valores faltantes. La característica 'Cabin' necesita más investigación, pero parece que podríamos querer eliminarla del conjunto de datos, ya que el 77% de los valores están faltantes.
En la imagen anterior puedes ver las 11 características más la variable objetivo (survived). ¿Qué características podrían contribuir a una mayor tasa de supervivencia de los pasajeros del Titanic? A mí me parece lógico que todas, excepto ‘PassengerId’, ‘Ticket’ y ‘Name’, estén correlacionadas con una mayor probabilidad de supervivencia de los pasajeros del Titanic.
Edad y Sexo 👶👩👨
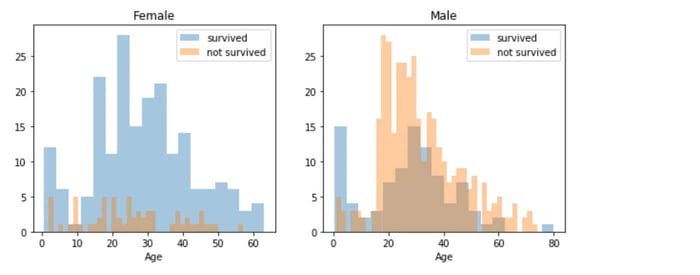
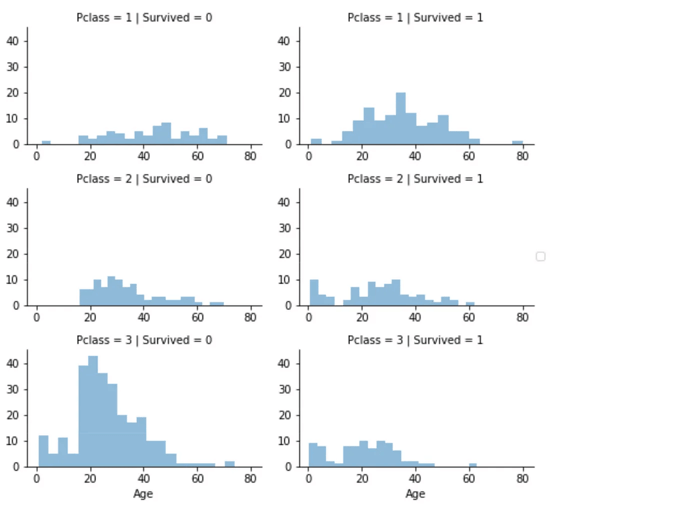
Como podemos ver, los hombres tienen una alta probabilidad de supervivencia cuando tienen entre 18 y 30 años, lo cual también es algo cierto para las mujeres, pero no completamente. Para las mujeres, las probabilidades de supervivencia son mayores entre los 14 y 40 años. Por otro lado, los hombres tienen una probabilidad de supervivencia muy baja entre 5 y 18 años, pero esto no es cierto para las mujeres. Además, los infantes también tienen algo más de probabilidad de sobrevivir.
Como parece que hay edades específicas que aumentan las probabilidades de supervivencia en los pasajeros del Titanic y debido a que quiero que todas las características estén en una escala similar, crearé grupos de edades más tarde.
Embarque, Clase y Sexo ⚓👩✈️
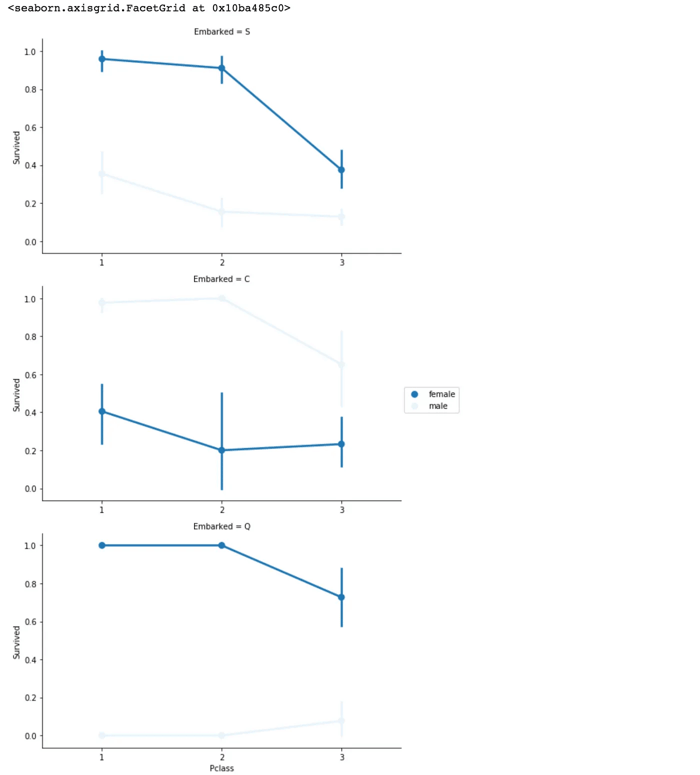
El puerto de embarque de los pasajeros del Titanic parece estar correlacionado con la supervivencia, dependiendo del sexo. Las mujeres en el puerto Q y el puerto S tienen una mayor posibilidad de supervivencia, mientras que es inverso en el puerto C. Los hombres tienen una alta probabilidad de supervivencia si están en el puerto C, pero una baja probabilidad en los puertos Q y S.
4.Pclass (Clase del Pasajero del Titanic) 🏷️
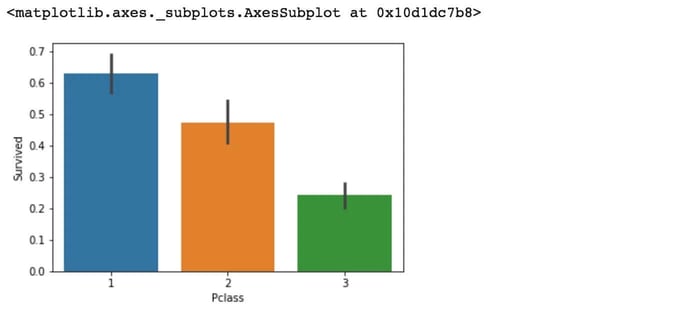
Aquí podemos ver claramente que la clase del pasajero (Pclass) del Titanic contribuye a las probabilidades de supervivencia, especialmente si la persona está en la clase 1. A continuación, crearemos otro gráfico que muestre cómo varía la supervivencia según la clase.
El gráfico anterior confirma nuestra suposición sobre la Pclass 1, pero también podemos observar una alta probabilidad de que una persona en Pclass 3 no sobreviva.
SibSp y Parch (Hermanos y Cónyuges / Padres e Hijos) 👨👩👧👦
Las características SibSp (número de hermanos y cónyuges a bordo) y Parch (número de padres e hijos a bordo) tienen más sentido como una característica combinada que muestra el número total de familiares de una persona en el Titanic. A continuación, crearé esta nueva característica y también una variable que indica si alguien no estaba solo en el barco Titanic .
A continuación, se muestra el gráfico que refleja la relación entre el número de familiares y la supervivencia:
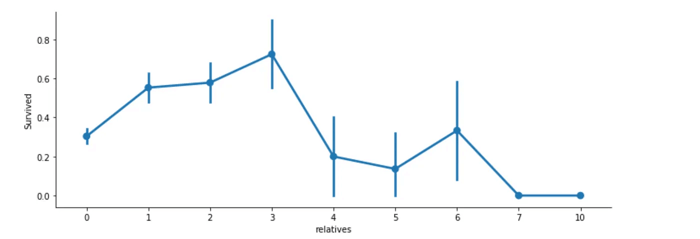
Aquí podemos ver que tenías una mayor probabilidad de sobrevivir con entre 1 y 3 familiares, pero una probabilidad menor si tenías menos de 1 o más de 3 (excepto en algunos casos con 6 familiares). Este análisis sugiere que los pasajeros del Titanic que tienen una familia a bordo puede influir en las probabilidades de supervivencia, aunque el impacto varía según la cantidad de familiares.
Preprocesamiento de los Datos 🛠️
Primero, eliminaré ‘PassengerId’ del conjunto de entrenamiento, ya que no contribuye a la probabilidad de supervivencia de una persona. No lo eliminaré del conjunto de prueba, ya que es necesario para la presentación de resultados.
Tratamiento de los Valores Faltantes 🛠️
Cabina: Como recordatorio, debemos tratar los valores faltantes de Cabin (687), Embarked (2) y Age (177). Primero pensé que tendríamos que eliminar la variable ‘Cabin’, pero después encontré algo interesante. Un número de cabina parece como ‘C123’, y la letra se refiere al puente. Por lo tanto, vamos a extraer estos valores y crear una nueva característica que contenga el puente de una persona. Posteriormente, convertiremos esta variable en un valor numérico. Los valores faltantes se convertirán en 0.
Edad: Ahora podemos abordar el problema de los valores faltantes en la edad. Crearé una matriz que contenga valores aleatorios, calculados a partir de la media de la edad en función de la desviación estándar y los valores nulos.
Embarque: Como la característica Embarked solo tiene 2 valores faltantes, simplemente los llenaremos con el valor más común.
Conversión de Características 🔄
train_df.info()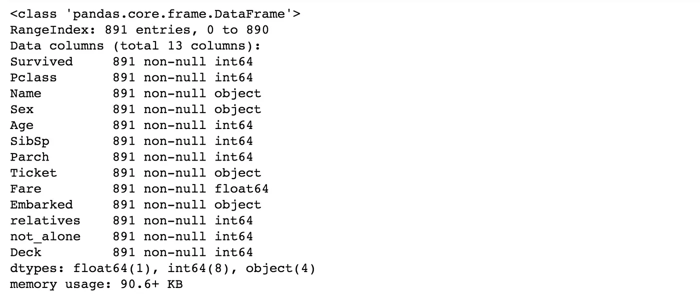
Arriba se puede ver que «Tarifa» es un valor decimal (float) y que debemos lidiar con cuatro características categóricas: Nombre, Sexo, Ticket y Embarque. Investiguemos y transformemos uno tras otro.
Nombre y Títulos de los Pasajeros 🏷️
Vamos a utilizar la característica Nombre para extraer los títulos del nombre, de modo que podamos construir una nueva característica a partir de esta información. A continuación, definimos los títulos y asignamos un valor numérico a cada uno:
Luego, para cada conjunto de datos, extraemos los títulos de los nombres, reemplazamos algunos títulos menos comunes por el valor "Rare", y convertimos los títulos en valores numéricos:
Finalmente, eliminamos la columna 'Name' del conjunto de datos, ya que ahora la información relevante sobre el título está representada en la nueva característica 'Title':
Este proceso convierte los nombres en títulos útiles, que pueden ser una buena característica para predecir la supervivencia de los pasajeros. Usamos títulos como Mr, Miss, Mrs, etc., y les asignamos valores numéricos para su procesamiento posterior.
Fare: Convertiremos ‘Fare’ de flotante a entero.
Sexo: Convertimos ‘Sex’ a un valor numérico.
Ticket: Dado que el atributo ‘Ticket’ tiene 681 tickets únicos, será complicado convertirlos en categorías útiles. Así que lo eliminaremos del conjunto de datos.
Embarked: Convertiremos el Puerto de ‘Embarked’ de los pasajeros del Titanic de dato categórico a numérico.
ports = {"S": 0, "C": 1, "Q": 2}
data = [train_df, test_df]
for dataset in data:
dataset['Embarked'] = dataset['Embarked'].map(ports)Creación de Categorías en las Características 🏷️
Edad (Age) 👶👴
Primero, vamos a convertir la característica ‘Age’. La convertiremos de flotante a entero y luego crearemos una nueva variable llamada ‘AgeGroup’, clasificando las edades en grupos. Es importante prestar atención a cómo formamos estos grupos, ya que no queremos que el 80% de los datos caigan en el primer grupo. Aquí te mostramos cómo hacerlo:
Este proceso divide la variable ‘Age’ en grupos de edad, lo que facilita el análisis y el aprendizaje automático. Ahora podemos ver cómo se distribuyen los grupos de edad en el conjunto de entrenamiento:
Tarifa (Fare) 💵
Para la característica ‘Fare’ (tarifa), necesitamos hacer lo mismo que con ‘Age’. Sin embargo, esto no es tan sencillo, porque si dividimos el rango de valores de la tarifa en categorías grandes, el 80% de los valores caerían en la primera categoría.
Afortunadamente, podemos utilizar la función “qcut()” de sklearn para dividir las tarifas en categorías de tamaño más equilibrado. Así formamos las categorías de la siguiente manera:
Este proceso categoriza las tarifas de los pasajeros en diferentes grupos basados en rangos específicos, lo que ayuda a entender mejor las variaciones en la tarifa y cómo influyen en la supervivencia de los pasajeros.
Creación de Nuevas Características ✨
Edad por Clase: Creamos una nueva característica combinando Edad y Pclass.
Tarifa por Persona: Creamos una nueva característica que muestra la tarifa pagada por persona.
Entrenamiento de Modelos de Aprendizaje Automático 🧠
Ahora entrenaremos varios modelos de aprendizaje automático y compararemos sus resultados. Dado que el conjunto de datos no proporciona etiquetas para el conjunto de prueba, utilizaremos las predicciones sobre el conjunto de entrenamiento para comparar los algoritmos entre sí.
Random Forest:
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_prediction = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)Logistic Regression:
logreg = LogisticRegression()
logreg.fit(X_train, Y_train)
Y_pred = logreg.predict(X_test)
acc_log = round(logreg.score(X_train, Y_train) * 100, 2)K Nearest Neighbor:
# KNN knn = KNeighborsClassifier(n_neighbors = 3) knn.fit(X_train, Y_train) Y_pred = knn.predict(X_test) acc_knn = round(knn.score(X_train, Y_train) * 100, 2)Gaussian Naive Bayes:
gaussian = GaussianNB() gaussian.fit(X_train, Y_train) Y_pred = gaussian.predict(X_test) acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2)Perceptron:
perceptron = Perceptron(max_iter=5)
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)Linear Support Vector Machine:
linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)
Y_pred = linear_svc.predict(X_test)
acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2)Decision Tree
decision_tree = DecisionTreeClassifier() decision_tree.fit(X_train, Y_train) Y_pred = decision_tree.predict(X_test) acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)Resultados de los Modelos 💡
Validación Cruzada K-Fold 🔄
Como podemos ver, el clasificador Random Forest ocupa el primer lugar. Pero antes, vamos a comprobar cómo se comporta Random Forest cuando utilizamos validación cruzada.
Validación Cruzada K-Fold
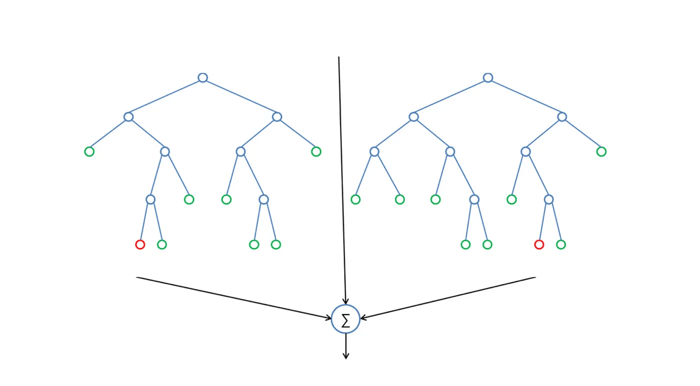
La validación cruzada K-Fold divide aleatoriamente los datos de entrenamiento en K subconjuntos llamados "folds". Imaginemos que dividimos los datos en 4 folds (K = 4). Nuestro modelo de Random Forest se entrenaría y evaluaría 4 veces, utilizando un fold diferente para la evaluación cada vez, mientras se entrena con los otros 3 folds.
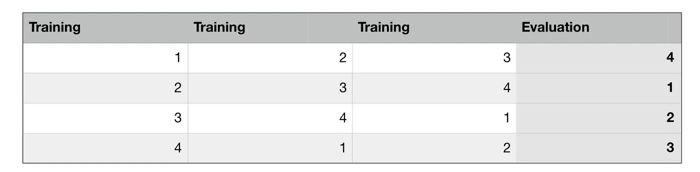
El proceso de validación cruzada K-Fold con 4 folds se ve en la siguiente imagen. Cada fila representa un proceso de entrenamiento y evaluación. En la primera fila, el modelo se entrena con los primeros tres subconjuntos y se evalúa con el cuarto. En la segunda fila, el modelo se entrena con el segundo, tercero y cuarto subconjunto y se evalúa con el primero. El proceso se repite hasta que cada fold actúa como un fold de evaluación.
El resultado de la validación cruzada K-Fold con 10 folds (K = 10) sería un array con 10 puntuaciones diferentes. A continuación, se muestra el código para realizar la validación cruzada:
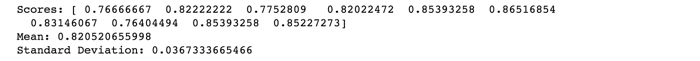Este resultado es mucho más realista que antes. Nuestro modelo tiene una precisión promedio del 82% con una desviación estándar de 4%. La desviación estándar nos muestra cuán precisas son las estimaciones. Esto significa que la precisión de nuestro modelo puede variar entre +/- 4%.
Creo que la precisión sigue siendo muy buena y, como Random Forest es un modelo fácil de usar, intentaremos mejorar su rendimiento aún más en la siguiente sección.
¿Qué es Random Forest? 🌲
Random Forest es un algoritmo de aprendizaje supervisado que analizamos en detalle en nuestro curso de Fundamentos Avanzados de Matemáticas para Machine Learning en Frogames Formación. Como su nombre indica, crea un "bosque" y lo hace de manera aleatoria. Este "bosque" está compuesto por varios árboles de decisión, generalmente entrenados con el método de bagging. La idea básica del método bagging es que una combinación de modelos de aprendizaje mejora el resultado general.
En pocas palabras, Random Forest construye múltiples árboles de decisión y los combina para obtener una predicción más precisa y estable.
Una gran ventaja de Random Forest es que puede ser utilizado tanto para problemas de clasificación como para regresión, que son los más comunes en los sistemas actuales de aprendizaje automático. Con algunas excepciones, un clasificador Random Forest tiene todos los hiperparámetros de un clasificador de árbol de decisión y también todos los hiperparámetros de un clasificador de bagging para controlar el conjunto de árboles.
El algoritmo de Random Forest introduce mayor aleatoriedad en el modelo cuando crece el árbol. En lugar de buscar la mejor característica al dividir un nodo, busca la mejor característica dentro de un subconjunto aleatorio de características. Este proceso genera una gran diversidad, lo que generalmente resulta en un mejor modelo.
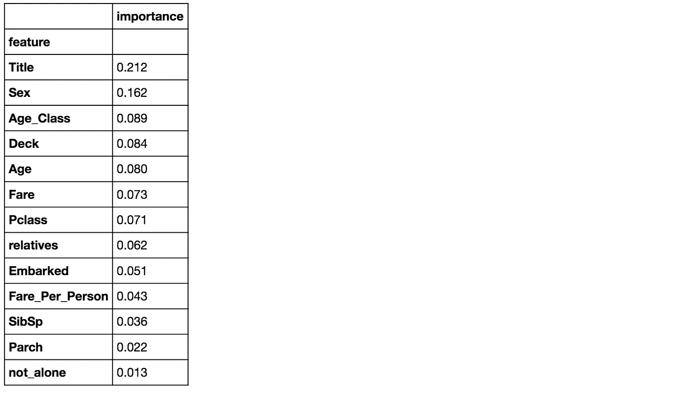
Importancia de las Características 📊
Otra excelente cualidad de Random Forest es que facilita la medición de la importancia relativa de cada característica. Sklearn mide la importancia de una característica observando cuánto reducen la impureza los nodos del árbol que usan esa característica (en promedio, a través de todos los árboles del bosque). Este puntaje se calcula automáticamente para cada característica después del entrenamiento y los resultados se escalan de modo que la suma de todas las importancias sea igual a 1.
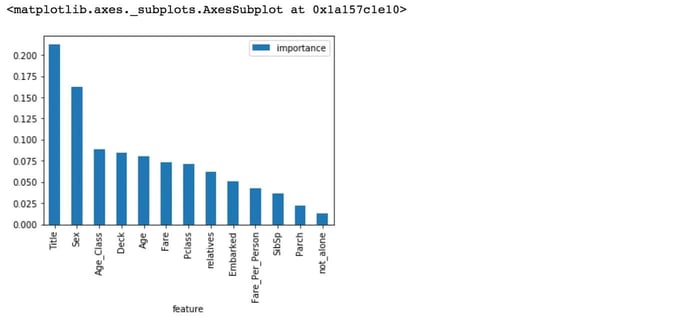
Conclusión: Eliminación de Características Innecesarias 🚮
Las características not_alone y Parch no desempeñan un papel significativo en el proceso de predicción de nuestro clasificador Random Forest. Por eso, las eliminaré del conjunto de datos y entrenaré nuevamente el clasificador.
Entrenamiento de Random Forest nuevamente:
Resultado: 92.82%
Nuestro modelo de Random Forest predice tan bien como antes. Una regla general es que, cuantas más características tengas, más probable será que tu modelo sufra de overfitting, y viceversa. Sin embargo, creo que nuestros datos están bien, ya que no contienen demasiadas características.
También existe otra forma de evaluar un clasificador Random Forest, que probablemente sea mucho más precisa que la puntuación que usamos antes. Me refiero a la estimación de error fuera de la bolsa (OOB) para estimar la precisión de generalización del modelo.
Resultado OOB: 81.82%
Ahora podemos empezar a ajustar los hiperparámetros de Random Forest.
Ajuste de Hiperparámetros 🔧
A continuación, te muestro el código para el ajuste de hiperparámetros, donde se optimizan parámetros como criterion, min_samples_leaf, min_samples_split y n_estimators.
Evaluación del Modelo y Medidas Adicionales 📏
Ahora que tenemos un modelo adecuado, podemos empezar a evaluar su rendimiento de una manera más precisa. Hasta ahora solo hemos utilizado la precisión y el puntaje OOB, que son formas de medir la precisión. Sin embargo, es más complicado evaluar un modelo de clasificación que uno de regresión. Discutiremos más sobre esto a continuación.
Matriz de Confusión 🔍
La primera fila se refiere a las predicciones de no sobrevivientes: 493 pasajeros fueron correctamente clasificados como no sobrevivientes (verdaderos negativos) y 56 fueron erróneamente clasificados como no sobrevivientes (falsos positivos). La segunda fila se refiere a las predicciones de sobrevivientes: 93 pasajeros fueron erróneamente clasificados como sobrevivientes (falsos negativos) y 249 fueron correctamente clasificados como sobrevivientes (verdaderos positivos).
Precisión y Recall
Precisión: 81% (porcentaje de veces que el modelo predijo correctamente la supervivencia de un pasajero)
Recall: 72% (porcentaje de personas que realmente sobrevivieron y fueron correctamente predichas)
F-Score
El F-Score es 0.76, lo que indica que el modelo tiene una combinación aceptable de precisión y recall, aunque no es perfecto. Este puntaje no es muy alto debido a que el recall es bajo (72%).
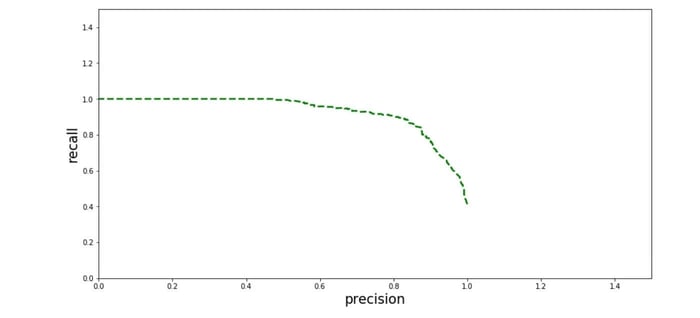
Curva de Precisión-Recall 📊
Para cada persona que el algoritmo de Random Forest clasifica, calcula una probabilida basada en una función y clasifica a la persona como sobreviviente (cuando la puntuación es mayor que el umbral) o como no sobreviviente(cuando la puntuación es menor que el umbral). Es por esto que el umbral juega un papel muy importante.
Vamos a graficar la precisión y el recall con el umbral utilizando matplotlib:
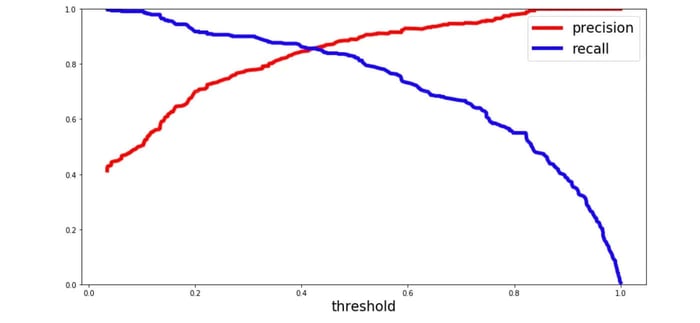
En el gráfico anterior, podemos ver claramente que el recall disminuye rápidamente cuando la precisión alcanza alrededor del 85%. Por lo tanto, es posible que desees seleccionar el punto de equilibrio entre precisión y recall antes de que la precisión alcance ese umbral, por ejemplo, alrededor del 75%.
Ahora puedes elegir un umbral que te proporcione el mejor trade-off entre precisión y recall para tu problema de aprendizaje automático. Si, por ejemplo, deseas una precisión del 80%, puedes observar en los gráficos que necesitarías un umbral de alrededor de 0.4. Luego, podrías entrenar un modelo con ese umbral y obtener la precisión deseada.
Otra forma de analizar el trade-off entre precisión y recall es graficando ambos valores contra cada uno:
Curva ROC AUC 🔍
Otra forma de evaluar y comparar tu clasificador binario es utilizando la Curva ROC AUC. Esta curva grafica la tasa de verdaderos positivos (también llamada recall) contra la tasa de falsos positivos (la proporción de instancias negativas clasificadas incorrectamente), en lugar de graficar la precisión contra el recall.
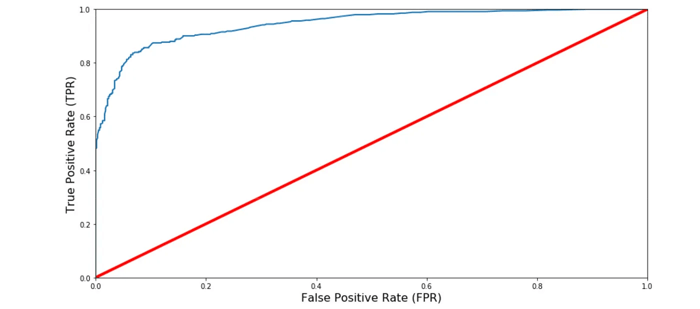
La línea roja en el centro representa un clasificador aleatorio puro (como un lanzamiento de moneda). Por lo tanto, tu clasificador debería alejarse lo más posible de esta línea. En nuestro caso, el modelo Random Forest parece funcionar muy bien.
Por supuesto, también tenemos un trade-off aquí, ya que el clasificador produce más falsos positivos a medida que aumenta la tasa de verdaderos positivos.
Puntuación ROC AUC 🏅
La puntuación ROC AUC es la puntuación correspondiente a la Curva ROC AUC. Se calcula midiendo el área bajo la curva, lo que se conoce como AUC. Un clasificador 100% correcto tendría una puntuación ROC AUC de 1, mientras que un clasificador completamente aleatorio tendría una puntuación de 0.5.
Resultado ROC-AUC Score: 0.9450
¡Perfecto! Creo que esta puntuación es lo suficientemente buena como para enviar las predicciones al leaderboard de Kaggle.
Resumen 📝
Comenzamos con la exploración de datos, donde nos familiarizamos con el conjunto de datos, verificamos los datos faltantes y aprendimos qué características son importantes. Durante este proceso, utilizamos Seaborn y Matplotlib para realizar las visualizaciones.
En la parte de preprocesamiento de datos, tratamos los valores faltantes, convertimos características en valores numéricos, agrupamos los valores en categorías y creamos algunas nuevas características.
Después, entrenamos 8 modelos diferentes de aprendizaje automático para predecir la supervivencia de los pasajeros del Titanic, seleccionamos uno de ellos (Random Forest) y aplicamos validación cruzada. A continuación, discutimos cómo funciona Random Forest, analizamos la importancia que asigna a las diferentes características y optimizamos su rendimiento ajustando los hiperparámetros. Finalmente, revisamos la matriz de confusión del modelo y calculamos la precisión, el recall y el F-score.
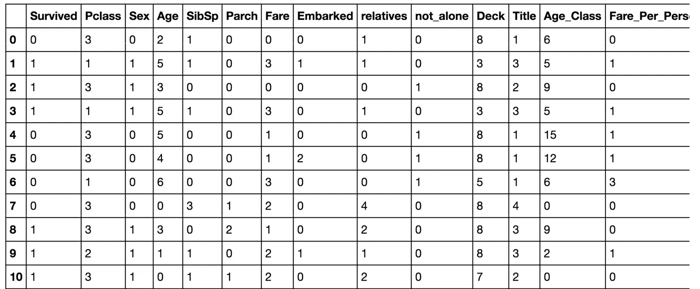
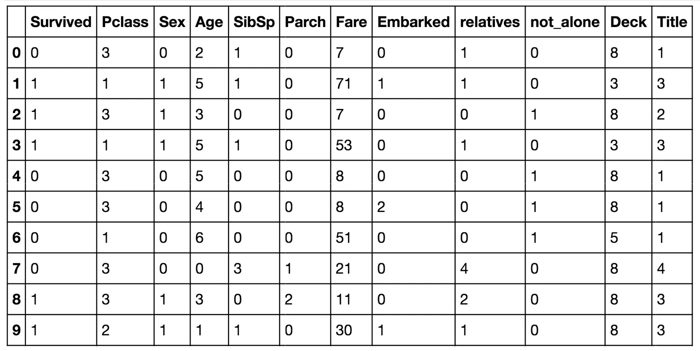
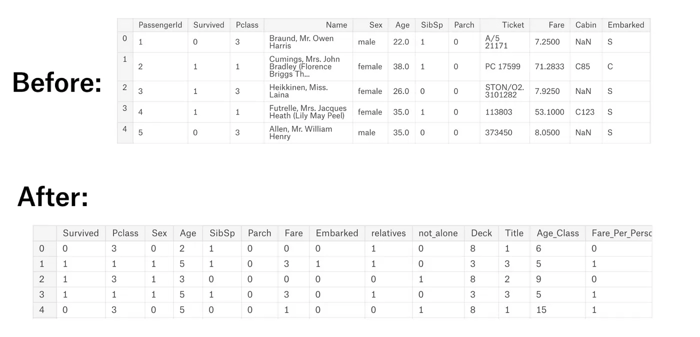
A continuación, se muestra una imagen del antes y después del dataframe “train_df”:
Mejoras y Oportunidades 🔧
Por supuesto, aún hay margen para mejorar la predicción de la supervivencia de los pasajeros del Titanic, como realizar una ingeniería de características más extensa, comparando y graficando las características entre sí e identificando y eliminando las características ruidosas.
Otra forma de mejorar los resultados del dataset de los Pasajeros del Titanic en el leaderboard de Kaggle sería realizar un ajuste de hiperparámetros más exhaustivo en varios modelos de aprendizaje automático. Además, podrías probar con aprendizaje en conjunto(ensemble learning) para mejorar la precisión general del modelo.
