Las ecuaciones diferenciales juegan un papel fundamental en la comprensión de muchos fenómenos de las ciencias, las matemáticas, la ingeniería, la economía e incluso las ciencias sociales. En matemáticas ayuda a mostrar la tasa de cambio de diferentes derivadas que juegan un papel crucial en la rama de las matemáticas del Cálculo. Por eso es importante conocer qué es una ecuación diferencial y para qué sirve.
Se utiliza en cálculo para resolver la ecuación que contiene una función desconocida “y=f(x)”. La solución de estas ecuaciones mediante el uso de una derivada se conoce como ecuación diferencial.
Estas soluciones brindan información sobre cómo cambian las cantidades y por qué ocurren este tipo de cambios. Para resolver las ecuaciones diferenciales se utilizan diferentes técnicas en diferentes formas, incluidas las soluciones directas y el uso de gráficas.
En este artículo, brindaremos el concepto detallado de ecuaciones diferenciales, qué es una ecuación diferencial, sus tipos, cómo se resuelven y por qué son cruciales en varios campos.
¿Qué es una ecuación diferencial?
Se puede responder a la pregunta qué es una ecuación diferencial diciendo que se trata de una ecuación matemática que involucra una función desconocida y derivadas de la variable dependiente con respecto a la independiente. Sus derivadas representan la tasa de cambio de esa función.
En general, una ecuación diferencial toma la forma:
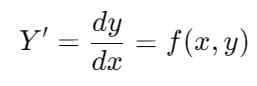
Donde “y” es la función desconocida que se escribe como y = f(x) e Y’ representa la derivada de la función según la variable “x”. La solución de la ecuación se escribe de esta forma:
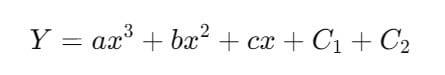
Donde, “a, b, c” son las constantes arbitrarias y C1 y C2 son la constante de integración. La solución particular se obtiene después de encontrar los valores de la constante integradora.
La función utilizada en la ecuación muestra alguna cantidad física y la ecuación diferencial relaciona esta función con su tasa de cambio. También nos ayuda a comprender cómo cambian las cosas en el tiempo o el espacio.
Por ejemplo: Si se estudia cómo cambia la temperatura de un objeto con el tiempo,
Luego, los modelos de ecuaciones diferenciales ayudan a mostrar la relación entre temperatura y tiempo.
Ayuda a relacionar el tasa de cambio de la temperatura a factores como la temperatura ambiente y otras condiciones que afectan al objeto. Este tipo de relación hace que las ecuaciones diferenciales sean muy valiosas para comprender los diferentes sistemas físicos.
Tipos de ecuaciones diferenciales
Las ecuaciones diferenciales se pueden clasificar en algunas categorías según sus características y el uso de variables independientes. También sobre la base de órdenes de derivados que intervienen en cualquier ecuación diferencial.
Ecuaciones diferenciales ordinarias (EDO): Se trata de funciones de una sola variable y sus derivadas. Por ejemplo, la velocidad de enfriamiento de una taza de café puede describirse mediante una EDO. La forma general de este tipo se puede expresar como:
F(x,y,y′,y′′,…,y(n))=0
Y La EDO simple de primer orden se puede escribir como:
dy/dx = f(x, y)
Ecuaciones diferenciales parciales (PDE): Este tipo involucra funciones de varias variables y sus derivadas parciales. Las PDE se utilizan para modelar sistemas más complejos, como la distribución de calor en una varilla de metal a lo largo del tiempo, y la forma general se expresa como:
F(x1,x2,…,xn,u,ux1,ux2,…,uxn,ux1x2,…) = 0
Y la PDE común de segundo orden, la ecuación de calor se puede expresar como:
∂u/∂t=α(∂2u/∂x2)
Lineal versus no lineal: Una ecuación diferencial se llama lineal si se puede escribir como una combinación lineal de la función desconocida y sus derivadas. Si no, es no lineal. Las ecuaciones diferenciales lineales suelen ser más fáciles de resolver. Mientras que la solución de no lineales requiere técnicas más avanzadas. La forma general de ambos se expresa como:
Lineal | No lineal |
an(x)y(n)+an−1(x)y(n−1)+⋯+a1(x)y′+a0(x)y = g(x) | y′′+y2=0 |
Homogéneo versus no homogéneo: Una ecuación diferencial es homogéneo si cada término involucra la función desconocida o sus derivadas. Si hay un término independiente de la función, la ecuación se llama no homogéneo.
Homogéneo | No homogéneo |
an(x)y(n)+an−1(x)y(n−1)+⋯+a1(x)y′+a0(x)y = 0 | an(x)y(n)+an−1(x)y(n−1)+⋯+a1(x)y′+a0(x)y = g(x) |
Métodos para resolver ecuaciones diferenciales
Para entender qué es una ecuación diferencial y resolverla, utilice los diferentes métodos según los tipos y valores de las condiciones iniciales. Su solución encuentra la función que satisface la relación dada que involucra sus derivadas. A continuación se detallan los métodos que se pueden utilizar para resolver ecuaciones diferenciales:
Separación de variables: Esta técnica se utiliza cuando la ecuación se puede organizar de modo que cada variable aparezca en un lado diferente de la ecuación.
Factores integradores: Este método se utiliza para ecuaciones diferenciales lineales de primer orden al encontrar los factores integrantes para convertir la ecuación a una forma más simple que pueda resolverse mediante integración.
Transformada de Laplace: Se utiliza para resolver ecuaciones diferenciales que involucran condiciones iniciales, especialmente en ingeniería y física. Por ejemplo: ecuación de calor, ecuación de onda, ecuación de circuito RC y muchas más.
Métodos numéricos: Si la ecuación se da en formas complejas, las soluciones analíticas son imposibles. Para ello se utilizan métodos numéricos como “método de Euler, método de Runge-Kutta” para encontrar la solución aproximada.
¿Cómo resolver las ecuaciones diferenciales?
Los diferentes tipos de ecuaciones adoptan diferentes métodos. Estos métodos se analizan anteriormente. Pero aquí discutimos cómo aplicar el método anterior al tipo respectivo de ecuación diferencial:
1. Ecuaciones separables
Este tipo de ecuaciones se pueden dar en la forma: “dy/dx = g(x) h(y)” y se pueden resolver siguiendo los pasos a continuación:
Reorganice la ecuación para separar variables como: 1/h(y) dy = g(x)dx.
Aplicar la integración en ambos lados y simplificar según las reglas de integración: ∫1/h(y) dy =∫g(x) dx.
Después de la integración, resuelva para “y” (si es posible).
2. Factor Integrador
En este tipo, la ecuación se da en forma de ecuación diferencial de primer orden y se expresa como:
dy/dx + P(x) y = Q(x)
Nota: si la ecuación no está dada en esa forma, primero hágala en esa forma.
Pasos para resolver:
Primero, encuentre el factor integrante (I.F) por la fórmula: μ(x) = e∫ P(x) dx.
Después de encontrar el valor I.F, multiplica por la ecuación completa:
µ(x). dy/dx + µ(x). P(x) y = μ(x).Q(x)
Establezca la derivada en el lado izquierdo: d/dx (μ(x)y) = μ(x)Q(x)
Aplica la integración en ambos lados y resuelve para "y".
3. Ecuaciones exactas
En este tipo, la ecuación se da en forma exacta que se puede expresar como:
M(x,y) + N(x,y) dy/dx = 0
Pasos para resolver:
Primero, verifica que la ecuación sea exacta si las derivadas parciales de M y N son iguales: ∂M/∂a = ∂N/∂x.
Si es exacta, entonces encuentre una función Ψ(x,y) tal que: ∂Ψ/∂x = M y ∂Ψ/∂y = norte
Por último, configure la función “Ψ(x,y) = C” para alguna constante "C".
Ejemplo de ecuaciones diferenciales
En esta sección, resuelva el ejemplo matemático usando la fórmula anterior de acuerdo con los tipos de la pregunta dada que ayuda a encontrar los valores de
Ejemplo 1: Encuentra la solución de la ecuación diferencial “ y' = 2x ”, si pasa por el punto (2, 7).
Solución:
Notamos que la ecuación dada tiene la forma de ecuación separable y encontramos su valor usando el método separable.
dy/dx = 2x
Paso 1: Separe las variables con “x” e “y”.
dy = 2x dx
Paso 2: Ahora, aplique la integración en ambos lados y simplifique usando la regla integradora.
∫dy = ∫2xdx
y = 2. x2/2 + C
y = x2 + C -------------> (i)
Paso 3: Ahora, encuentre el valor de la constante "C" usando el valor del punto.
y = 7, x = 2
Ponga la ecuación (i) que se convierte en:
7 = (2)2 +C
7 = 4 + C
C = 7 - 4 = 3
Así la ecuación (i) queda después de poner “C”.
y = x2 + 3
Alternativamente, y tras entender qué es una ecuación diferencial, para superar el largo proceso manual, utilice una calculadora de ecuaciones diferenciales. Esta calculadora en línea gratuita proporciona el resultado de cualquier tipo de ecuación en cuestión de segundos después de ingresar los valores en los campos de entrada indicados.
Ejemplo 2: Encuentra la solución de la ecuación diferencial “dy/dx + y = 2x” mientras pasa por el punto (0, 1).
Solución:
La ecuación dada es una ecuación diferencial ordinaria lineal de primer orden, que se puede resolver utilizando el método del factor integrante. La ecuación dada ya está en forma estándar, por lo que nos saltamos el primer paso y avanzamos.
dy/dx + y = 2x
Paso 1: Encuentra el factor integrante de la ecuación dada.
μ(x)=e∫P(x)dx = e∫1 dx = ex
Paso 2: Multiplica I.F con la ecuación anterior.
ex dy/dx + ex y = 2x. ex
Paso 3: Haz la derivada en el lado izquierdo y aplica la integración para simplificar la ecuación.
d/dx (exy) = 2x.ex
∫ {d/dx(exy)}dx = ∫2x. ex dx
exy = ∫2x. ex dx
Usando la fórmula para integración por partes para resolver la integral del lado derecho.
exy = ∫2xex dx = 2x ex −∫2exdx = 2xex − 2ex + C
Paso 4: Dividir por “ex ” en ambos lados y aplique el valor de los puntos para encontrar la constante “c”.
y = 2x – 2 + C.e−x ------------------> (i)
x = 0, y = 1
1 = 2(0) − 2 + C e(0)
C = 1 + 2 = 3
Por tanto, la solución final de una ecuación diferencial.
y = 2x−2+3e−x
¿Por qué son importantes las ecuaciones diferenciales?
Las ecuaciones diferenciales son esenciales porque ayudan a resolver los diferentes modelos y comprender los diferentes ejemplos de vida en el mundo. Los procesos naturales implican tasas de cambio y las ecuaciones diferenciales nos brindan una forma única de expresar estos procesos matemáticamente.
Diseño de ingeniería: Los ingenieros utilizan ecuaciones diferenciales para diseñar sistemas que sean seguros y eficientes. La estabilidad de un puente, la trayectoria de vuelo de una aeronave o la funcionalidad de un circuito eléctrico dependen de ecuaciones diferenciales.
Modelado de enfermedades: En medicina, las ecuaciones diferenciales se utilizan para predecir la separación de enfermedades infecciosas. El modelo SIR (susceptibles, infectados y recuperados) para predecir brotes, lo que permite a los funcionarios de salud pública tomar medidas oportunas.
Predicción climática: Las ecuaciones diferenciales son cruciales en la modelización climática. Ayuda a los científicos a predecir escenarios climáticos futuros, basándose en datos actuales de temperatura, humedad y presión.
Conclusión
Las ecuaciones diferenciales son una parte esencial de las matemáticas para describir sistemas dinámicos. Ayudan a explicar cómo cambian las cosas y a predecir resultados futuros basándose en datos actuales y pasados.
Al predecir la propagación de enfermedades, comprender las tendencias económicas o diseñar la próxima nave espacial, las ecuaciones diferenciales ayudan a resolver los sistemas más complejos en la resolución de problemas del mundo real.
Ya seas ingeniero, biólogo, economista o simplemente un estudiante curioso, comprender las ecuaciones diferenciales abre la puerta a una amplia gama de aplicaciones en el mundo en el que vivimos.
¡Nos vemos en clase!